Ostrosłup prawidłowy czworokątny. Poprawkowicz: W ostrosłupie prawidłowym czworokątnym przekątna podstawy ma długość 8√6 cm. Pole jednej ściany bocznej tego ostrosłupa jest równe polu podstawy ostrosłupa. a)Krawędź podstawy ostrosłupa d=8{6} a√2=8√6 a=8√3 b) Wysokość ściany bocznej No to a²=192 PΔ=192

1
	*a*h=192
2

a*h=384 I co dalej?

Poprawkowicz:

Mila: Co masz obliczyć?

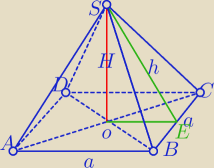Mila: |AC|=p=8√6 P_BCS=P_ABCD 1) a√2=8√6 /*√2 2a=8√12 a=8√3 2) P_ABCD=a²=64*3=192

1
	a*h=192
2

1
	*8√3*h=192⇔4√3*h=192
2

√3*h=48 /*√3 h=16√3 3) W ΔSOE: H²+|OE|²=h²⇔H²+(4√3)²=256*3 H²=720 H=√720=√36*4*5 H=12√5

	1
V=		*a2*H
	3

	1
V=		*192*12√5
	3

V=768√5[j³] ============

Poprawkowicz: Dzięki, głupi błąd w równaniu miałem.