zad
omikoron: Wykaż, że dla dowolnych dodatnich liczb rzeczywistych x i y takich, ze x2+y2=2 prawdziwa
jest nierówność x+y≤2
16 gru 17:32
Maciek: Wykaż. że √2−x2+x≤2
16 gru 17:35
omikoron: wyjdzie −2x2+4x−2≤0
16 gru 17:42
omikoron: ?
16 gru 17:43
Satan: I teraz rysunek zrób.
16 gru 17:43
omikoron: zał. x≠2 i 2−x>0 wiec x<2
czyli ostatecznie bedzie x∊R\{2}
16 gru 17:45
piotr: Δ=16−16=0 ⇒x∊D∊<−√2; √2>
16 gru 17:48
Satan: Chwila. Skąd założenie x ≠ 2 i 2−x > 0?
16 gru 17:48
omikoron: x0= −b/2a
16 gru 17:50
piotr:
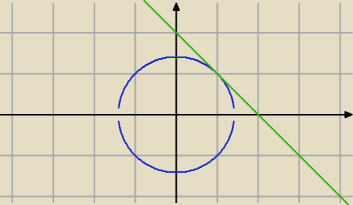
16 gru 17:50
omikoron: (√2−x2)2≤(2−x2) nierowność mozna podnosic do kwadratu jesli obie strony sa dodatnie
wiec musi byc załozenie
16 gru 17:53
omikoron: wystarczy ten rysunek bo teraz nwm
16 gru 18:03
omikoron:
16 gru 22:03
