Planimetria i zadanie z wykorzystaniem optymalizacji Satan: Przeciwprostokątna trójkąta prostokątnego ma długość 5. Wyznacz długości jego przyprostokątnych, tak aby kwadrat wysokości tego trójkąta poprowadzonej z wierzchołka kąta prostego miał największą wartość. Szczerze powiedziawszy, to nie za bardzo wiem jak to rozgryźć. Jakieś sugestie?

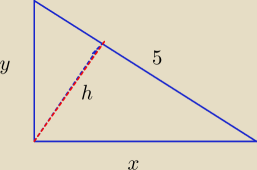
iteRacj@: h>0, x>0, y>0

1		1
	*x*y =		*5*h
2		2

5*h = x*y

	x*y
h =
	5

z tw.Pitagorasa 5² = x² + y², 0<x<5 y² = 25 − x² , y= √25 − x²

	x*√25 − x2
h =
	5

	x2*(25 − x2)
h2 =
	25

	x2*(25 − x2)
czyli f(x) =
	25

i teraz musisz znaleźć maksimum tej funkcji dla 0<x<5

Satan: Czyli byłem blisko, już wiem czego mi zabrakło... Dziękuję iteRacj@!