Zadanie
Lol: x2−11|x| + 30 = 0
2 lut 19:19
Mickej: rozpisz to na 2 przypadki
x<0 i x≥0
rozpisujesz jak zwykłe równanie z wartością bezwzględną
2 lut 19:27
Lol: czyli tak: x2−11|x|+30 <0 i x2−11|x| + 30 ≤0 ?
2 lut 19:30
Mickej: nie
2 lut 19:32
Mickej:
x2−11x+30=0 gdy x≥0
x2+11x+30=0 gdy x<0
2 lut 19:33
Godzio: dodam że jest to częściowe przekształcenie względem OY, także można by było i takim sposobem
2 lut 19:37
Julek: po co rozpisywać na przypadki ?
Od razu można zauważyć, że to x
2−11x+30 po symetrii częściowej OY
liczymy...
x
2−11x+30 =0
Δ = 121 − 120 = 1
2
x
3=−x
1 = −5
x
4=−x
2 = −6
x∊{−6;−5;5;6}
2 lut 19:37
Julek: Zgadzam się z Godziem
2 lut 19:38
Godzio:
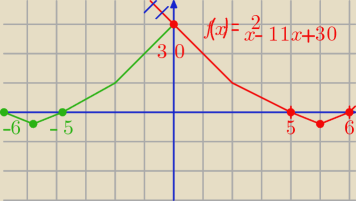
rysujemy wykres
f(x) = x
2 − 11x + 30
( x
1=5,x
2=6, p = 5,5, q=−1/4, f(0) = 30)
wymazujemy lewą stronę i odbijamy to co zostało po prawej względem OY
2 lut 19:45
Lol: aaaahaa, no tak dzięki
2 lut 19:46
Julek:
Godzio, papuga
2 lut 19:48
Godzio:
nudziło mi się i narysowałem
2 lut 19:49