zad
say: Okrąg o promieniu 4 jest wpisany w trójkąt. Punkt styczności podzielił jeden z boków na odcinki
o długości 6 i 8. Oblicz długości boków tego trójkąta.
14 gru 22:13
===:
zrób rysunek i będzie jaśniej

14 gru 22:18
say: dzieki
14 gru 22:24
===:
dodatkowa podpowiedź ... twierdzenie o dwusiecznej

14 gru 22:29
Janek191:
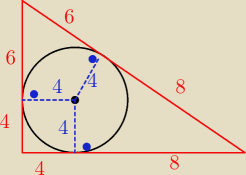
14 gru 22:45
Eta:
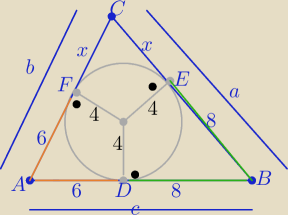
1/ z twierdzenia o odcinkach stycznych
| | 28+2x | |
2/ P=rp , p= |
| = 14+x |
| | 2 | |
P=4(14+x) ⇒ P
2=16(14+x)
2
3/ ze wzoru Herona
P=
√p(p−a)(p−b)(p−c) ⇒ P=
√(14+x)*6*8*x ⇒ P
2=48(14+x)*x
to 16(14+x)
2= 48(14+x)*x ⇒ 14+x=3x ⇒
x=7
długości boków trójkąta : a=15, b=13, c=14
14 gru 22:51
Janek191:
Zły rysunek

14 gru 22:52
say: dzieki

14 gru 23:18



 1/ z twierdzenia o odcinkach stycznych
1/ z twierdzenia o odcinkach stycznych

