f kwadratowa hzek: Wykres funkcji kwadratowej f(x) przechodzi przez punkty (−2,16), (1,−2), (3,6). Po przesunieciu go o wektor V=[2,−6] i przekstalceniu przez symetrie wzgledem prostej x=0 otrzymano wykres funkcji g(x). Wykres funkcji g(x) przeszktalcono przez symerie wzgledem prostej y=3, otrzymując wykres funkcji h(x). Napisz wzory funkcji f(x), g(x) i h(x). Pomoże ktoś?

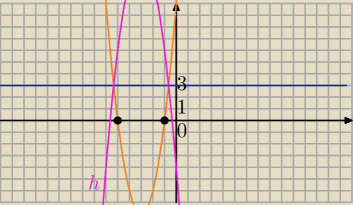
Mila: 3) Symetria względem prostej y=3 [B[g(−x)=y=2x²+12x+10] x'=x y'=−y+3*2⇔y'=−y+6⇔y=−y'+6 podstawiamy do wzoru funkcji −y'+6=2x'²+12x'+10 −y'=2x'²+12x'+4 y'=−2x'²−12x'−4 opuszczamy znaczki h(x)=−2x²−12x−4 II sposób h(x)=0 ⇔x=−5 lub x=−1 A=(−5,0), B=(−1,0) p=−3 q=−8 W=(−3,−8) Znajdujesz obrazy tych punktów i rozwiązujesz jak w punkcie (1)

Mila: Pierwsze dwa punkty nie weszły mi . Może za chwilę edytor namyśli się, albo wyślę bez rysunków.

Mila: 1) f(x)=ax²+bx+c f(−2)=16⇔a*4+b*(−2)+c=16 f(1)=−2⇔a+b+c=−2 f(3)=6⇔a*9+b*3+c=6 Mamy układ równań: 4a−2b+c=16 a+b+c=−2 9a+3b+c=6 ======== (1)−(2) i (3)−(2) 3a−3b=18 8a+2b=8 ========= a−b=6 4a+b=4 ======dodajemy stronami 5a=10⇔a=2 8+b=4⇔b=−4 2−4+c=−2⇔c=0 f(x)=2x²−4x 2) Translacja o wektor v=[2,−6] t(x)=f(x−2)−6=2(x−2)²−4*(x−2)−6 t(x)=2x²−12x+10 Symetria względem OY g(−x)=2x²+12x+10 3) symetria względem prostej y=3 w następnym wątku

hzek: Dziekuje Mila!

Mila: