oblicz całkę
Filip:
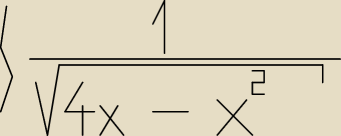
Oblicz całkę.
Kurcze nie wiem jak się za ten przykład zabrać pomoże ktoś

13 gru 22:00
kochanus_niepospolitus:
| | 1 | | 1 | |
∫ |
| dx = // t = x−2 −> x = t+2 ; dt = dx // = ∫ |
| dx = |
| | √x(x−4) | | √(t−2)(t+2) | |
| | dt | | t | | x−2 | |
= ∫ |
| = arcsin |
| + C = arcsin |
| + C |
| | √t2−4 | | 2 | | 2 | |
13 gru 22:03
kochanus_niepospolitus:
warto zapamiętać to przejście
13 gru 22:04
Filip: SUPER DZIĘKI
13 gru 22:08
Filip: ale tam jest x(x−4) a po podstawieniu jest sam kwadratu różnicy zniknął x. Może tak być

13 gru 22:19
kochanus_niepospolitus:
| | 1 | | t | |
tak jest ... i masz później ∫ |
| dt = arcsin |
| |
| | √4 − t2 | | 2 | |
popełniłem dwa błędy które się 'zniosły'

13 gru 22:26
Filip: aha
13 gru 22:26
Filip:
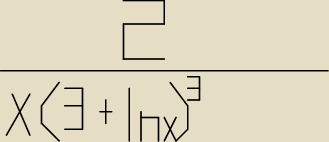
Została mi ostatnia ale chyba najtrudniejsza bo w ogóle nie wiem jak się za nią zabrać
13 gru 22:39
Mariusz:
t=3+lnx
Co do pierwszej całki to warto zapamiętać następujące podstawienia
1. a>0
√ax2+bx+c=t−√ax
Wyznaczasz z podstawienia x jako funkcję zmiennej t
a następnie różniczkujesz stronami
W razie potrzeby wyznaczasz też z podstawienia pierwiastek
2. a<0
Tutaj możesz założyć że b2−4ac>0
i sprowadzić trójmian kwadratowy pod pierwiastkiem do postaci iloczynowej
a następnie stosujesz podstawienie
√a(x−x1)(x−x2)=(x−x1)t
Wyznaczasz z podstawienia x jako funkcję zmiennej t
a następnie różniczkujesz stronami
W razie potrzeby wyznaczasz też z podstawienia pierwiastek
Chociaż powyższe dwa podstawienia wystarczą do sprowadzenia całki postaci
∫R(x,√ax2+bx+c)dx do funkcji wymiernej to
jednak istnieje jeszcze jedno podstawienie √ax2+bx+c=xt+√c c>0
które czasami może prowadzić do całki wymagającej mniej obliczeń
14 gru 19:52
 Oblicz całkę.
Kurcze nie wiem jak się za ten przykład zabrać pomoże ktoś
Oblicz całkę.
Kurcze nie wiem jak się za ten przykład zabrać pomoże ktoś


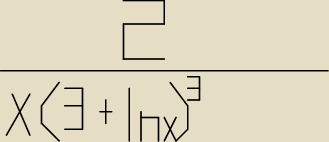 Została mi ostatnia ale chyba najtrudniejsza bo w ogóle nie wiem jak się za nią zabrać
Została mi ostatnia ale chyba najtrudniejsza bo w ogóle nie wiem jak się za nią zabrać