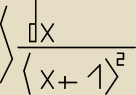Oblicz całkę metodą przez podstawienie
∫dx(x+1)2
| dt | t−2+1 | t−1 | −1 | |||||
∫ | = ∫ t−2dt = | + C = | + C = | + C = | ||||
| t2 | −2+1 | −1 | t |
| −1 | ||
+ C | ||
| x+1 |
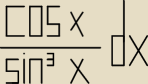a coś takiego
cosxsin(3)x
| dt | t−3+1 | t−2 | −1 | |||||
∫ | = ∫ t−3 dt = | + C = | + C = | + C = | ||||
| t3 | −3+1 | −2 | 2t2 |
| −1 | 1 | −1 | ||||
* | + C = | + C | ||||
| 2 | t2 | 2sin2x |