Prosze o pomoc
Kasia: Podaj liczbe rozwiazan rownania w zaleznosci od parametru m.
|logx2|+4=m2
13 gru 18:43
ale jak to?: Narysuj sobie wykres i otrzymasz:
brak rozwiązań : m2<4
1 rozwiązanie: m=4
2 rozwiązania m2>4
jeśli źle rozumuję to proszę, niech ktoś to poprawi
13 gru 19:58
Kasia: W odpowiedziach jest inaczej 😣
13 gru 20:05
Mila:
Co masz w odpowiedzi?
13 gru 20:07
PW: ale jak to? Jeżeli m=4, to mamy równanie
|logx2| = 0,
skąd
x2 = 1
− a to równanie ma dwa rozwiązania.
13 gru 20:18
PW: Korekta. Miało być: Jeżeli m2=4.
13 gru 20:25
ale jak to?: czekaj, czekaj...
Na chłopski rozum.
Jeśli m=2 v m=−2 to wówczas mamy
|logx2|+4=4
|logx2|=0
logx2=0
2logx=0logx=0
x=1 jedno rozwiązanie
dla m ∊ (−2,2) brak rozwiązania − wartość bezwzględna nie może być ujemna
czyli dla m ∊ (−∞,−2) u (2,+∞) − dwa rozwiązania
czy tak masz w odp?
13 gru 20:30
Kasia: 0 rozwiazan dla m € (−2;2)
2 dla m € {−2,2}
4 dla m € (−nieskończoności;−2)U(2;+nieskończoności)
13 gru 20:31
ale jak to?: dobra wiem już co zrobiłem źle wcześniej, powinno być:
y=m2
Dla:
y < 4 −> brak rozwiązań
y = 4 −> 1 rozwiązanie
y > 4 −> 2 rozwiązanie
podstawiając za y=m2 rozwiązujemy przedziały dla jakich m równanie jest spełnione
13 gru 20:33
PW: ale jak to, błąd w rozumowaniu polega na przejściu od
logx2=0
do
2logx=0.
13 gru 20:34
ale jak to?: Kasia a definicja logarytmu logab=c , gdzie b>0 ? nie możemy mieć wartości ujemnej x w tym
zadaniu
13 gru 20:36
Dawid: A nie mozna podnieść wszystkiego do potegi 1/2, aby otrzymac log|x|+2=m?
13 gru 20:37
PW: Możemy, możemy.
x2>0
dla wszystkich x (z wyjątkiem zera).
13 gru 20:37
ale jak to?: PW, ale dlaczego, przecież są to prawa działań na logarytmach, obowiązujące w algebrze, której
się uczymy. Gdzie popełniłem błąd w rozumowaniu?
13 gru 20:38
PW: Dawidzie, tu już pojechałeś...
13 gru 20:38
PW: Błąd polega na tym:
− dziedziną równania
log2x=0
są wszystkie liczby rzeczywiste bez zera, a dziedziną równania
2logx=0
tylko liczby dodatnie.
Wzór
logxk = klogx
jest prawdziwy tylko dla x>0. Wzory trzeba znać nie tylko "obrazkowo", ale łącznie z
założeniami.
Stary Zrzęda
13 gru 20:45
Kasia: Czyli wychodzi mi |2logx|+4=m2 i nie za bardzo wiem co mam dalej z tym zrobić, jak bym nie
próbowała nie widze tu 4 rozwiązań
13 gru 20:48
ale jak to?: No ok, rozumiem to co napisałeś i bardzo jestem Ci wdzięczny za tą wypowiedź.
Ale w zadaniu jednak nie było uwzględnione dziedziny dla x ... więc sam nie wiem co o tym
myśleć.
Ale dziękuję za wytłumaczenie

13 gru 20:49
PW: Mateńko, tłumaczę, że nie wolno stosować wzoru
logx2=2logx.
Dalej już nie będę powtarzał, bo zacznę rzucać kredą.
13 gru 20:51
PW: To ostatnie było do Kasi

13 gru 20:52
Mila:
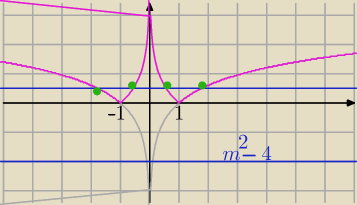
Wykres trochę sfuszerowany, edytor dorysował odgałęzienie u góry w lewo.
|logx
2|=m
2−4
x≠0
1)
m
2−4= 0
m=2 lub m=−2 dwa rozwiązania
2)m
2−4<0 ⇔
m∊(−2,2) brak rozwiązań
3) m
2−4>0⇔
m<−2 lub m>2 − 4 rozwiązania
Przykład:
|logx
2|=10
log x
2=10 lub logx
2=−10
x
2=10
10 lub x
2=10
−10
| | 1 | | 1 | |
x=105 lub x2=−105 lub x= |
| lub x=− |
| |
| | 105 | | 105 | |
13 gru 20:52


 Wykres trochę sfuszerowany, edytor dorysował odgałęzienie u góry w lewo.
|logx2|=m2−4
x≠0
1)
m2−4= 0
m=2 lub m=−2 dwa rozwiązania
2)m2−4<0 ⇔
m∊(−2,2) brak rozwiązań
3) m2−4>0⇔
m<−2 lub m>2 − 4 rozwiązania
Przykład:
|logx2|=10
log x2=10 lub logx2=−10
x2=1010 lub x2=10−10
Wykres trochę sfuszerowany, edytor dorysował odgałęzienie u góry w lewo.
|logx2|=m2−4
x≠0
1)
m2−4= 0
m=2 lub m=−2 dwa rozwiązania
2)m2−4<0 ⇔
m∊(−2,2) brak rozwiązań
3) m2−4>0⇔
m<−2 lub m>2 − 4 rozwiązania
Przykład:
|logx2|=10
log x2=10 lub logx2=−10
x2=1010 lub x2=10−10