Obliczanie pola trójkąta i jego promieni Pq: W trójkącie dwa boki mają długość 3cm i 4 cm. Długość trzeciego boku jest większa od długości każdego z dwóch pozostałych boków. Długości wysokości w tym trójkącie są trzema kolejnymi wyrazami ciągu arytmetycznego. Oblicz pole tego trójkąta oraz promieni okręgów: wpisanego w ten trójkąt i opisanego na tym trójkącie

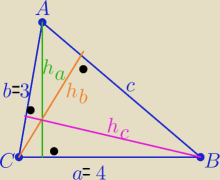
Eta: c>a>b to h_b>h_a>h_c i h_b, h_a, h_c −−− tworzą ciąg arytm ⇒ 2h_a=h_b+h_c

	2P		2P		2P
ha=		, hb=		, hc=
	a		b		c

	2P		2P		2P
zatem 2*		=		+
	4		3		c

	1		1		1
		=		+		⇒ c=6
	2		3		c

długości boków trójkąta : a=4, b= 3, c=6 ze wzoru Herona :

	a+b+c
P=√p(p−a)(p−b)(p−c) =..... , gdzie p=
	2

	2P
r=		=....
	a+b+c

	abc
R=		=.....
	4P

Rogalik: 3,4,x − ciąg arytmetyczny, x>4 r = 4−3=1 x=4+1 = 5 3,4,5 − trójkąt prostokątny na podstawie twierdzenia odwrotnego do twierdzenia Pitagorasa W trójkącie prostokątnym środek okręgu opisanego na nim znajduje się w środku przeciwprostokątnej. Czyli R = 5:2 = 2,5 cm (długość promienia okręgu opisanego na trójkącie). Długość promienia okręgu wpisanego łatwo obliczyć korzystając ze wzoru na pole trójkąta: P = 1/2 * 3*4 =6 P = r * (a+b+c)/2 6 = r*(3+4+5)/2 6=r*6 r=1

Eta: W treści zadania napisane: długości wysokości tworzą ciąg arytmetyczny

Rogalik: Oj... To wysokości miały tworzyć ciąg:( Zagapiłem się:( i rozwiązałem swoje zadanie...