Symetralna odcinka Pq: Napisz równanie symetralnej odcinka o końcach A = (−2,−3) B= (−4,−5).

the foxi: Symetralna przechodzi przez środek odcinka pod kątem prostym

	−2−4		−3−5
Środek=(		;		)=(−3;−4)
	2		2

	−5+3
Odcinek jest częścią prostej o współczynniku kierunkowym a=		=1
	−4+2

Zatem symetralba ma postać y=ax+b, gdzie a=−1 i do niej należy punkt Środek −5=−x+b −5=4+b b=−9 y=−x−9

the foxi: Ajajajaj machnąłem się. −4=3+b b=−7 y=−x−7

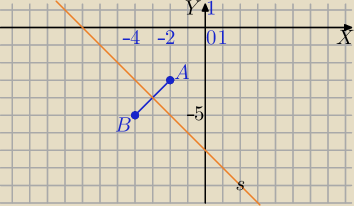
Mila: A = (−2,−3) B= (−4,−5). Symetralna odcinka to zbiór wszystkich punktów jednakowo odległych od końców odcinka. P(x,y)− dowolny punkt symetralnej. √(x+2)²+(y+3)²=√(x+4)²+(y+5)²⇔ (x+2)²+(y+3)²=(x+4)²+(y+5)² po wykonaniu działań i redukcji s: y=−x−7