Zdarzenia losowe Nieznane: Prawdopodobieństwo zdania egzaminu przez ucznia uczącego się na bieżąco wynosi 0,95, a nie uczącego się na bieżąco 0,15. Wiadomo, że w klasie 60 % uczniów uczy się na bieżąco. 1. Jakie jest prawdopodobienstwo, że uczeń zda egzamin? 2. Jeden z uczniów zdał egzamin, jakie jest prawdopodobieństwo, że uczeń ten uczył się na bieżąco?

iteRacj@: Jakie jest prawdopodobienstwo, że losowo wybrany uczeń zda egzamin? 0,6*0,95 + 0,4*0,15

iteRacj@: P(Z) − prawdopodobieństwo, że losowo wybrany uczeń zda egzamin P(Z) = 0,6*0,95 + 0,4*0,15 = 0,63 P(U) − prawdopodobieństwo, że losowo wybrany uczeń się uczy na bieżąco P(U) = 0,6 P(ZIU) − prawdopodobieństwo, że uczeń zda egzamin pod warunkiem, że się uczy na bieżąco

	P(Z∩U)
P(ZIU) = 0,95 =
	P(U)

stąd P(Z∩U) = P(ZIU)*P(U) P(UIZ) − prawdopodobieństwo, że uczeń uczy się na bieżąco, jeśli wiadomo (=pod warunkiem), że zdał egzamin

	P(U∩Z)		P(Z∩U)		P(ZIU)*P(U)		0,95*0,6
P(UIZ) =		=		=		=
	P(Z)		P(Z)		P(Z)		0,63

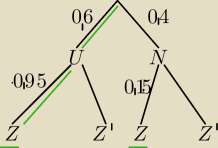
Mila: a) A− losowo wybrany uczeń zda egzamin P(A)=0.6*0.95+0.4*0.15=0.63 b) uczeń zdał egzamin, jakie jest prawdopodobieństwo, że uczeń ten uczył się na bieżąco?

	0.6*0.95		57
P(U/A))=		=		≈0.9
	0.63		63

iteRacj@: a jednak można prościej niż ja, to dobra wiadomość