trygonometria
kami: nie wiem jak sie zabrać
| | π | | π | |
2cos2(x+ |
| )−3sin( |
| −x)>1 z jakiego wzoru skorzystać, próbuje z 1 dać cos i wyłączyć |
| | 4 | | 3 | |
sin przed nawias ale to mi nic nie daje, kąty są rózne więc nie mam pojęcia może sin2α
12 gru 19:41
5-latek: sin(π/3−x)= cos (π/2−(π/3−x))
12 gru 19:45
kami: rozumiem ze to wstawiam pod sin nie wspomnę ze nie wiem skąd się to wzięło 90
0−30
0?
| | π | | π | |
wyszło 2cos2(x+ |
| )−3cos( |
| +x)>1 |
| | 4 | | 6 | |
poczekam może ktoś jaśniej wyjasni
12 gru 20:03
kami: czy mogłby ktoś pomóc ?
12 gru 20:18
kami: help
12 gru 20:46
Mila:
Dobrze to przepisałaś? Z jakiego zbioru?
12 gru 21:22
kami: z głowy profesora
i jak patrzę to jest dobrze przepisane, kolega ma tak samo i tez nie wie
jak zrobic
12 gru 21:29
kami: Powiem tak kumpel ma 5 z matmy i nie rozwiązał ale jak Mila nie daje rady to ja zamiatam i idę
spać
12 gru 21:46
Eta:
| | π | | π | |
2cos2(x+ |
| )−1 >3sin( |
| −x) |
| | 4 | | 3 | |
| | π | | π | |
cos(2x+ |
| > −3sin(x− |
| ) |
| | 2 | | 3 | |
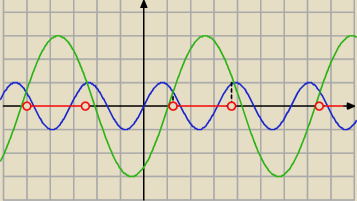
rozwiązania zaznaczone na wykresie
12 gru 21:47
Eta:
2cos2α−1= cos(2α)
12 gru 21:48
kami: dzięki
spróbuję przeanalizować
12 gru 21:51
ale jak to?: na pewno trzeba skorzystać ze wzorów:
cos(α+β)=cosαcosβ−sinαsinβ
sin(α−β)=sinαcosβ−cosαsinβ
12 gru 21:53
Eta:
A Twój profesor niech odczyta.... x
12 gru 21:54
kami: skąd −3sin dlaczego minus ?
12 gru 21:56
kami: wiem już nie trzeba wyjaśniać
12 gru 21:57
Eta:
sin(−α)= −sinα
| | π | | π | |
3sin( |
| −x)= −3 sin(x− |
| ) |
| | 3 | | 3 | |
12 gru 21:57
Eta:
12 gru 21:58
kami: tak tak wiem, teraz te punkty rozkminiam
12 gru 22:02
Mila:
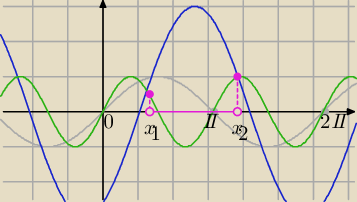
Trudno znaleźć dokładne wartości.
cos(2x)=2cos2x−1
| | π | | π | |
2cos2(x+ |
| )=cos(2x+ |
| )+1=−sin(2x)+1 |
| | 4 | | 2 | |
| | π | |
−sin(2x)+1−3sin( |
| −x)>1 |
| | 3 | |
Odczytujcie dla jakich x niebieski wykres leży nad zielonym.
w przedziale <0,2π>
coś około (?)
1,2<x<3.8
12 gru 22:05
Eta:
Mila
czytaj wpis 21: 47
12 gru 22:12
Mila:
No to jesteśmy zgodne w zeznaniach
12 gru 22:16
Eta:
12 gru 22:17
kami: no fakt beznadziejnie mi się odczytuje
nawet mimo wykresu
12 gru 22:19
Mila:
Masz popielaty wykres, aby zaznaczyć: π i 2π.
π≈3.14
x1 trochę mniejszy od π, a x2 większy od π.
T=2π
12 gru 22:37
Mila:
| | π | |
x1 trochę mniejszy od |
| |
| | 2 | |
12 gru 22:37
kami: ok zobaczę co jutro sor wykombinuje dzięki MIla
12 gru 22:48
Eta:
12 gru 22:49