geometria art22: ZAD2 Pole przekroju osiowego stożka jest trójkątem równobocznym o polu 36√3 cm. Oblicz V i P powierzchni całkowitej. ZAD3 Oblicz V stożka, w którym pole powierzchni bocznej wynosi 72π cm², a promień podstawy stanowi połowę długości tworzącej.

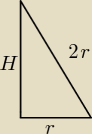
puk: Zad 3. P_b = 72π cm² 72π = πrl 72π = πr(2r) 2r² − 72 = 0 r² − 36 = 0 (r + 6)(r −6) = 0 , r> 0 ⇒ r = 6cm H² + r² = (2r)² H² = 4r² − r² H² = 3r²/ √ H = √3r Masz już wszystko. Resztę dokończ sam. Zad 2.

	a2√3
36√3 =		/ * 4 , : √3
	4

144 = a² /√ , (pamiętamy że a> 0) a = 12

	a
r =
	2

r = 6

	a√3
H =
	2

H = 3√3 l² = H² + r² Oblicz l i będziesz miał już wszystko. Resztę jesteś w stanie dokończyć samemu.

Łukasz: moim zdaniem jest pomyłka , ponieważ H=6√3