Stereometria Jacek: W sześcianie o krawędzi długości 1 dm wyznaczono punkty K, L i M , które są środkami trzech, parami skośnych, krawędzi sześcianu. Oblicz pole trójkąta KLM.

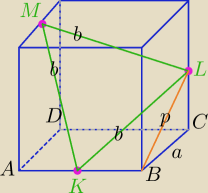
Mila: a=1dm ΔKLM− Δrównoboczny 1) W ΔBCL:

	1		5a2
p2=a2+(		a)2=
	2		4

2) W ΔKBL:

	1
b2=(		a)2+p2
	2

	6a2		3a2
b2=		=
	4		2

3)

	b2√3		3a2√3
PΔKLM=		⇔ PΔKLM=
	4		8

	3√3
PΔKLM=		dm2
	8

======================

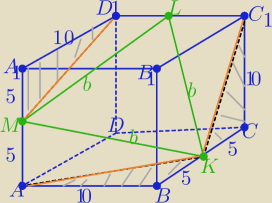Eta: 1/ΔKLM jest równoboczny o boku długości "b" 2/ z tw. Pitagorasa w ΔABK : |AK|²=|MD₁|²=|KC₁|²= 10²+5²=125 3/ w ΔAKM : |MK|²=b²= 5²+125 = 150 ⇒ b²=150

	b2√3		75√3
4/ P(KLM)=		=		dm2
	4		2

=========

Eta:

	75√3		3√3
Odp: P(KLM)=		cm2 =		dm2 ( jak u Mili
	2		8

Jacek: Dzięki wielkie