Ostrosłup Maciek: Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość 6, a krawędź boczna ma długość 12. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek rozłącznej z nią krawędzi bocznej. Oblicz pole ottrzymanego przekroju

	a*h
tak więc pole przekroju to		a=6, 62+(3√3)2 = h2 => h=√63 , h=3√7
	2

	18√7
P =		= 9√7 a w odpowiedzi jest 9√5, jest ktoś w stanie wskazać u mnie błąd?
	2

Maciek: up

Mila: Błędnie obliczona h. Nie widzę Twojego rysunku, ale chyba stosujesz tw. Pitagorasa do Δ, który nie jest prostokątny. Wychodzi wynik 9√5.

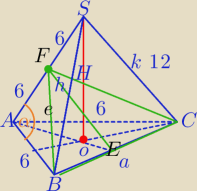
Mila: 1) W ΔABS: 12²=6²+12²−2*6*12*cosα

	1
cosα=
	4

2) W ΔAFB: e²=6²+6²−2*6*6*cosα e²=54 3) W ΔFBE: e²=h²+|BE|² 54=h²+3² h²=45 h=3√5 4)

	1
PΔBCF=		*6*3√5
	2

P_ΔBCF=9√5 ===========

Maciek: Racja, popełniłem ten błąd. W punkcie b miałem wyliczyć cos kątu nachylenia przekroju do podstawy, finalnie mi wyszło z tw. cosinusów, ale pierw próbowałem innym sposobem, jest ktoś w stanie wskazać co założyłem źle? Bo nie mogę się dopatrzeć błędu w obliczeniach http://scr.hu/3mbd/mnrg5