schemat hornera
hania: witam. mógłby mi ktoś wytłumaczyć tak jakoś prosto schemat hornera?
2 lut 16:05
Mateusz:
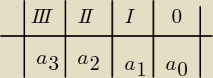
A patrzyłaś tu masz dobrze wyjasnione ja tylko dodam że
Na początek nalezy narysowac tabele o takiej liczbie kolumn jaki jest najwyzszy stopien
wielomianu bez względu na to czy są wszystkie pozostałe czy nie np jesli mamy wielomian
stopnia 3−ego np 3x
3+2x
2−4x+5 i dziele go np przez dwumian (x−1) i tabela wyglądac będzie
tak jak na rysunku w miejsce a
1 a
2 a
3 a
0 wpisujemy współczynnikiwielomianu dalsze
wypełnbianie tabelki polecam kliknąc w link jest swietnie wyjasnione
2 lut 16:22
2 lut 16:22
hania: dzięki

2 lut 16:43
AS:
Dany wielomian
W(x) = a
ox
n + a
1x
n−1 + a
2x
n−2 + ... + a
n−1x + a
n
dzielimy przez (x − α) otrzymując wielomian stopnia niższego
| W(x) | | r | |
| = V(x) + |
| |
| x − α | | x − α | |
gdzie V(x) = b
ox
n−1 + b
1x
n−2 + ... + b
n−2x + b
n−1
W(x) = V(x)*(x − α) + r
a
ox
n + a
1x
n−1 + a
2x
n−2 + ... + a
n−1x + a
n =
= ( b
ox
n−1 + b
1x
n−2 + ... + b
n−2x + b
n−1)*(x − α) + r
Wymnażając prawą stronę i porównując współczynniki mamy
a
0 = b
o b
o = a
o
a1 = b1 − α*b
o b1 = a
1 + α*bo
a
2 = b
2 − α*b
1 b
2 = a
2 + α*b
1
...............................................................
an = r − α*b
n−1 r = an + α*b
n−1
Przykład
(x
4 − 3*x
3 + 6*x − 5):(x + 2)
a
o = 1 , a
1 = −3 , a
2 = 0 , a
3 = 6 , a
4 = −5 , α = −2
b
o = a
o = 1
b
1 = a
1 + α*b
0 = −3 −2*1 = −5
b
2 = a
2 + α*b
1` = 0 −2*(−5) = 10
b
3 = a
3 + α*b
2 = 6 − 2*10 = −14
b
4 = a
4 + α**b
3 = −5 − 2*(−14) = 23 (reszta)
| | 23 | |
Wynik dzielenia: x3 − 5*x2 + 10*x − 14 + |
| |
| | x + 2 | |
2 lut 17:56
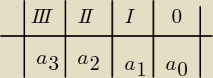 A patrzyłaś tu masz dobrze wyjasnione ja tylko dodam że
Na początek nalezy narysowac tabele o takiej liczbie kolumn jaki jest najwyzszy stopien
wielomianu bez względu na to czy są wszystkie pozostałe czy nie np jesli mamy wielomian
stopnia 3−ego np 3x3+2x2−4x+5 i dziele go np przez dwumian (x−1) i tabela wyglądac będzie
tak jak na rysunku w miejsce a1 a2 a3 a0 wpisujemy współczynnikiwielomianu dalsze
wypełnbianie tabelki polecam kliknąc w link jest swietnie wyjasnione
A patrzyłaś tu masz dobrze wyjasnione ja tylko dodam że
Na początek nalezy narysowac tabele o takiej liczbie kolumn jaki jest najwyzszy stopien
wielomianu bez względu na to czy są wszystkie pozostałe czy nie np jesli mamy wielomian
stopnia 3−ego np 3x3+2x2−4x+5 i dziele go np przez dwumian (x−1) i tabela wyglądac będzie
tak jak na rysunku w miejsce a1 a2 a3 a0 wpisujemy współczynnikiwielomianu dalsze
wypełnbianie tabelki polecam kliknąc w link jest swietnie wyjasnione
