parametr 00000: Dla jakich wartości parametru m rozwiązania x₁, x₂ równania 2x²−2(2m+1)x+m(m−1)=0 spełniają warunek x₁<m<x₂?Jakie tu będą założenia? Na pewno Δ>0, ale co z drugim? Jak to zapisać?

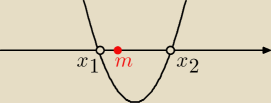
iteRacj@: drugi warunek f(m) <0 czy to dobry pomysł?

00000: Mnie się proszę nie pytać

00000: Czy pasowałoby: 1. Δ>0 2. x₁<m −−−> x₁−m<0 x₂>m −−−−> x₂−m>0 czyli (x₁−m)(x₂−m)<0 ?

Jerzy: Warunki: 1) Δ > 0 2) f(m) < 0 wystarczają w zupełności.

00000: A dałoby się jakoś ze wzorami Viete'a? Nie rozumiem jak zrobić ten drugi warunek f(m) < 0 i skąd on się w ogóle bierze

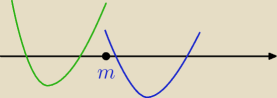
Jerzy: Zauważ,że gdyby f(m) ≥ 0 , to albo jeden z pierwiastków byłby dokładnie równy m lub obydwa pierwiastki leżałyby poza m ( z prawej lub lewej strony).Patrz rysunek.

Jerzy: Jak zrobić warunek: f(m) <0 , prosto: f(m) = 2m² − 2(2m +1)*m + m(m − 1) < 0

00000: Czyli skoro wiem, że wartość dla m jest ujemna, to tak jakby podstawiam m za x i dalej normalnie liczę?

Jerzy: Masz napisane wyżej, jak rozwiazać drugi warunek.

00000: ok, dziękuję