Trygonometria Mery: Argumenty w przedziale <−π;π> funkcji y=sinx

	√2
Gdy y=−
	2

Moje roz:

	√2
sinx=−
	2

	π
sinx=−sin
	4

	π
sinx=sin(−		)
	4

więc wychodzi mi

	π		5		π
x=π−(−		)+2kπ=		π+2kπ lub x=−		+2kπ ; k∊C
	4		4		4

	π
Więc w tym przedziale znajduje się argument x=−
	4

Moja odpowiedź jest niezgodna z tą ze zbioru, gdzie mam więc błąd?

Mila:

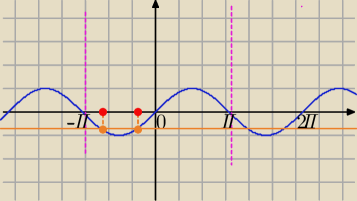
	√2
sinx=−		i x∊<−π,π>
	2

	5π		7π
x=		+2kπ lub x=		+2kπ
	4		4

k=0

	5π		7π
x=		∉D lub x=		∉D
	4		4

k=−1

	5π		3π		7π		π
x=		−2π=−		lub x=		−2π= −
	4		4		4		4

Mery: Dziękuję za rozwiązanie Ale czemu mój sposób na rozwiązanie jest zły?