pierwiastek z liczby zespolonej prosze: Proszę o sprawdzenie czy dobrze robię: Znajdź ³√z wiedząc że: (√3 + i)²(1 − i√3)⁴ * z = (1 + i)¹² + (−i)¹⁰ (−i)¹⁰ = i¹⁰ = (−1)⁵ = −1

	−(1+i)12
zatem z =
	(√3 + i)2(1 − i√3)4

po wykonaniu działań z mianownika:

	−(1+i)12		(1+i)12
z =		=
	−64		26

i teraz nakładam ³√ i mnożę razy kolejne pierwiastki trzeciego stopnia z jedynki: 1

	1		√3
−		+		i
	2		2

	1		√3
−		−		i
	2		2

	(1+i)4
w0 =		* 1 ;
	22

	(1+i)4		1		√3
w1 =		* −		+		i ;
	22		2		2

	(1+i)4		1		√3
w2 =		*−		−		i ;
	22		2		2

CZY SPOSÓB ROZWIĄZANIA JEST POPRAWNY ? ? ?

Mila: (1+i)¹²=[(1+i)²]⁶=(2i)⁶=64 (√3+i)²=3+2i√3−1=2+2i√3=2(1+i*√3) 2(1+i√3)*(1−i√3)⁴=2*(1−i²*3)*(1−√3*i)³= =8*(−8)=−64 −64*z= co masz z prawej? (1+i)¹²+(−i)¹⁰ ?

prosze: miało być * z prawej, przepraszam

Mila: No to masz proste. −64z=−64 z=1 ³√1 umiesz policzyć ?

prosze: tak. Nie wiem czemu mi wyszło z = −1

Mila: Dobrze Ci wyszło. Ja , zgubiłam (−) P=(1+i)¹²*(−i)¹⁰=−64*(−1)=64 −64*z=64 /:(−64) z=−1 ³√−1 policz, po kolacji sprawdzę, albo pomogę.

piotr: mi wychodzi: −64 z = −65

Mila: Piotrze tam z prawej ma być mnożenie.

prosze: piotr ja źle przepisałem, na początku jest *(−i)¹0, a nie + polecono mi zapamiętać kolejne pierwiastki drugiego, trzeciego, czwartego i szóstego stopnia z jedynki, to sobie skorzystam: w₀: −1*(1) = −1

	1		√3		1		√3
w1: −1*(−		−		i) =		+		i
	2		2		2		2

	1		√3		1		√3
w2: 1*(−		+		i) =		−		i
	2		2		2		2

albo: dla −1 argument wynosi π więc po podstawieniu do wzoru na pierwiastki: |z| = 1

	π		π		1		√3
dla k = 0 → w0: 1*(cos		+ isin		) =		+		i
	3		3		2		2

	π + 2π		π + 2π
dla k = 1 → w1: 1*(cos		+ isin		) = −1
	3		3

	π + 4π		π + 4π		π		π
dla k = 2 → w2: 1*(cos		+ isin		) = cos		− isin		=
	3		3		3		3

	1		√3
		−		i
	2		2

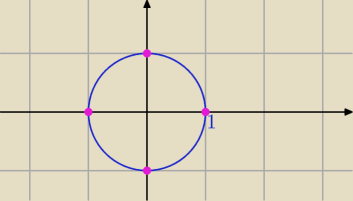Mila: ⁴√1 z₀=1 z₁=i z₂=−1 z₃=−i

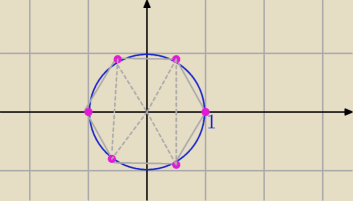Mila: ⁶√1

	1		√3		1		√3		1		√3		1		√3
zk∊{1,		+		i, −		+		i,−1,−		−		i,		−		i}
	2		2		2		2		2		2		2		2

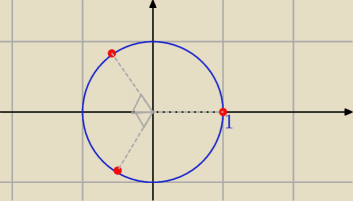
Mila: Na płaszczyźnie zespolonej pierwiastki n−tego stopnia z jedności są wierzchołkami wielokąta foremnego o n bokach wpisanego w okrąg jednostkowy, którego jeden z wierzchołków leży w punkcie 1. Realizują one podział tego okręgu na n równych części. ³√1

	1		√3		1		√3
zk∊{1, −		+		i , −		−		i}
	2		2		2		2

prosze: dziękuję za odpowiedzi i życzę miłego wieczoru

Mila: mam nadzieję, że przyda się.