Dowód trapez równoramienny Tomasz: Twierdzenie: W trapezie równoramiennym o podstawach mających długości a, b (a>b) wysokość poprowadzona z wierzchołka kąta rozwartego dzieli dłuższą podstawę na odcinki, których długości są równe (a+b)/2 i (a−b)/2. Udowodnij to twierdzenie. Proszę o wskazówki lub rozwiązanie.

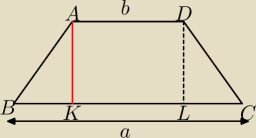
Fistaszek_99: Więc tak: AB=DC Wysokość poprowadzona z wierzchołka kąta rozwartego AK=h, pomocniczo poprowadziłem również wysokość DC. AK=DL

	a−b
BK=LC=
	2

	a−b		a−b		2b+a−b		a+b
czyli BK=		, a KL=b+		=		=
	2		2		2		2