stererometria maturzysta: Zad 1. Podstawą graniastosłupa prostego jest romb. Pola przekrojów tego graniastosłupa płaszczyznami zawierającymi przeciwległe przekątne podstaw są równe 36 i 48. Oblicz pole powierzchni boczej tej bryły. Zad 2. Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a. Objętość tego

	a3√3
ostrosłupa jest równa		Wyznacz cos kąta płaskiego przy wierzchołku ostrosłupa
	12

W 2 doszedłem, że H=a, środek trójkąta rownobocznego znajduje się 1/3h od podstawy więc z

	a√3		2√3a2
pitagorasa mam a2 + (		)2 =d2 => d=		i z twierdzienia cosinusów
	3		3

wychodzi mi cos α= 23/24 a ma wyjść 5/8

wmboczek: W 2 normalnie wychodzi 5/8, masz dobrze do tw cos trójkąt d,d,a Z1. Przekształcając wzór na Pb otrzymasz 2√36²+48²=120

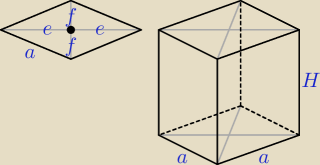
Bogdan: 2e*H = 48, 2f*H = 36,

	24		18
e =		, f =
	H		H

	242 + 182
a2 = e2 + f2 =		⇒ aH = √ 242 + 182 = 30
	H2

Pole powierzchni bocznej graniastosłupa P = 4aH = 4*30 = 120