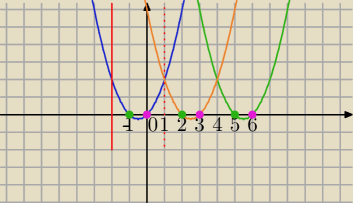
Funkcja okresowa Tomek: Dana jest funkcja okresowa f o okresie pods T=3, określona w przedziale <−2:1) wzorem f(x)=x² + x. Oblicz sumę wszystkich dodatnich miejsc zerowych funkcji f mniejszych od 100. Jest jakiś szybszy sposób niż dodawanie wszystkich miejsc zerowych po kolei ?

Tomek: Mógłby ktoś pomóc ?

Tomek: Proszę

Tomek: 3333

Mila: a₁=2, b₁=3 dodatnie wyrazy początkowe a_k=2+3(k−1), b_m=3+3(m−1) ciągi arytmetyczne, r=3 1) 2+3(k−1)<100 2+3k−3<100⇔3k<101

	101
kmax=[		]=33
	3

a₃3=2+3*32=98 2) 3+ 3(m−1)<100⇔3m<100 m_max=33 b₃3=3+3*32=99 4)

	2+98
S33(a)=		*33=50*33=1650
	2

	3+99
S33(b)=		*33=51*33=1683
	2

5) S=3333 ========= posprawdzaj, bo może coś źle przepisałam z kartki.

Tomek: Dziękuję <3

Mila: