Geometria analityczna UczącySię: Na prostej k o równaniu x − 3y −3 = 0 wyznacz punkt B tak, aby pole trójkąta ABC, gdzie A (−4,1) C(4,8) było równe 35. Użyłem wzoru na pole mając współrzędne trzech punktów i wyszły mi dwie możliwości współrzędnych, ale nei wiem co dalej ... mam sprawdzić czy pasują do prostej ?

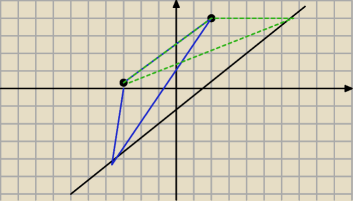
iteRacj@: są dwa takie trójkąty o polu 35, więc sprawdź pola, obliczając je

UczącySię: Ale mnie nie pytają o pola, tylko o współrzędne punktu ... Ja sobie to policzyłem ze wzoru na pole i mam tak: 7x_b − 12y_b = 30 lub 7x_b − 12 y_b = −110. Tutaj nie wiem co dalej

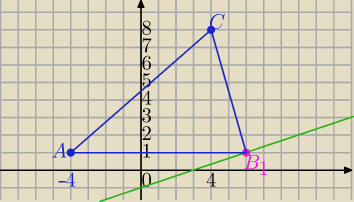
Mila: k: x − 3y −3 = 0

	x0
B∊k⇔B=(x0,		−1)
	3

A(−4,1) C(4,8) AC^→=[8,7]

	x0		x0
AB→=[x0+4,		−1−1]=[x0+4,		−2]
	3		3

	1		x0
PΔACB=		*|8*(		−2)−7*(x0+4)|
	2		3

1		13
	*|		x0+44|=35
2		3

13		13
	x0+44=70 lub		x0+44=−70
3		3

	342		−101
x=6 i y=1 lub x=−		i y=
	13		13

Nie musisz sprawdzać, ale: Sprawdzamy pole Δ AC^→[8,7] AB^→[10,0]

	1
P=		*|8*0−7*10|=35
	2

lub

	342		114		290		140
AB→=[−		+4,−		−2]=[−		, −		]
	13		3		13		13

	1		140		290		1		1120		2030
P=		*|8*−		−7*(−		)|=		|−		+		|=
	2		13		13		2		13		13

	1		910
P=		*		=35
	2		13

I po problemie.

UczącySię: No przecież, dzięki Mila i iteRacj@