Rozwiązanie geometryczne i optymalne ... gierki09: Zakład produkuje dwa wyroby, które są obrabiane na dwóch obrabiarkach: O₁ i O₂ i na frezarce F. Czas pracy tych maszyn jest ograniczony i wynosi dla obrabiarki O₁ − 18 000 maszynogodzin, dla obrabiarki O₂ − 40 000 maszynogodzin, a dla frezarki F − 24 000 maszynogodzin. Zużycie czasu pracy maszyn ( w godz.) na produkcję jednostki każdego z wyrobów podano w tabeli. Maszyna | Zużycie czasu pracy... I II O₁ 3 1 O₂ 2 4 F 3 2 Zysk ze sprzedaży wyrobu I wynosi 6 zł, a ze sprzedaży wyrobu II − 4 zł. 1. Zaplanować optymalną strukturę produkcji z punktu widzenia maksymalizacji zysku. (Zbudować model matematyczny zagadnienia i rozwiązać go metodą geometryczną). 2. Czy rozwiązanie optymalne ulegnie zmianie, jeżeli: a) zyski jednostkowe ze sprzedaży obydwu wyrobów wzrosną o 1 zł, b) dodatkowo uwzględni się warunek, że wyrobu II należy produkować 1,5 raza więcej niż wyrobu 1? Jak rozwiązać podpunkt 2 a) b)

kochanus_niepospolitus: a) zapewne tak ... pokaż jak wygląda wykres b) to już prawie na pewno, bo zapewne I produkujesz więcej niż II

gierki09: Trzy nierówności przekształciłem na 3 proste : y₁ = −3x + 18000 y₂ = −0,5x + 10000 y₃ = −1,5x + 12000 Z tych prostych wyszedł 5−kąt, gdzie punkt A(2000,9000) i B(4000,6000) są optymalnym rozwiązaniem dla zysku firmy i w obu przypadkach podstawiając do zysku (6x + 4y = c) wyszło c= 48 000, ale nie mam pojęcia jak zabrać się za podpunkt 2 a) b).

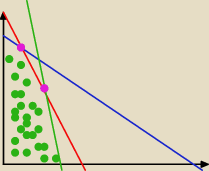
gierki09: Czerwone − y₃ Zielone − y₁ Niebieski − y₂ Różowe kropki to A(górna) i B(dolna)

gierki09: Punkty na osiach X i Y co 1000 zrobiłem.

kochanus_niepospolitus: no to teraz: 2a) rysujesz 7x + 5y = c'

kochanus_niepospolitus: 2b)

	3
rysujesz prostą: y =		x
	2

i wybierasz optymalne rozwiązanie leżące na tej prostej (bo ona zapewnia wskazaną proporcję)

gierki09: jak narysować prostą z 3 niewiadomymi?

gierki09: Bo to 7x + 5y = c' to nowy zysk, a my zysk obliczaliśmy z punktów skrajnych wielokąta, które były przecięciami prostych.

kochanus_niepospolitus: wyliczasz c' tak samo jak wcześniej przeliczone zostało c

kochanus_niepospolitus: tak naprawdę to robisz w taki sposób: rysujesz 7x+5y = 35000 po czym linijką przesuwasz tą prostą ku brzegu

gierki09: Wyszło mi, że wyrobu I − 4000, wyrobu II − 6000, a rozwiązanie optymalne czyli to c' ulegnie zmianie z 48 000 na 58 000.