Czy jest różniczkowalna ktoś: Jak sie sprawdzało czy funkcja jest różniczkowalna? Mam funckje 0, x<0 f(x) = 5x, x∊ <0,2) 10, x>2 I jest pytanie czy jest ona rozniczkowalan w przedziale ( −∞, ∞)

kochanus_niepospolitus: 1) czy jest ciągła 2) czy f'(x⁻₀) = f'(x₀) = f'(x⁺₀)

Rogalik: Nie jest. Wystarczy podać przykład. x1=4 i x2= 6 , (x1≠x2) f(4)=10 f(6)=10 zatem pokazaliśmy, że dla dwóch różnych iksów (argumentów) funkcja przyjmuje ta sama wartość, czyli nie jest różnowartościowa.

Rogalik: O przepraszam, źle spojrzałem:( miało być różniczkowalna

ktoś: No jakbym miał w punkcie to bym wiedział co zrobić z tym drugim warunkiem. Ale tutaj jest w całym przedziale. To może muszę tutaj sprawdzić granice obustronnie dla x=0, x=2?

kochanus_niepospolitus: ktoś −−− funkcja ta na pewno jest różniczkowalna w przedziałach: (−∞,0) (bo jest to funkcja stała f(x) = 0) (0, 2) (bo jest to funkcja prosa f(x) = 5x) (2, +∞) (bo jest to funkcja stała f(x) = 10) więc zostaje tylko kwestia czy funkcja ta jest różniczkowalna dla x=0 i x=2. To są jedyne dwa miejsca gdzie funkcja ta może nie być różniczkowalna

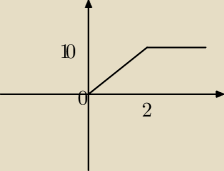
ktoś: 10, x≥2 miało być. Widać teraz, że funkcja jest ciagła. I co dalej mam zrobic z wiedzą ze jest ciagla?

kochanus_niepospolitus: Napisałem Ci drugi warunek, który wystarczy na to, aby wykazać, że ta funkcja nie jest różniczkowalna w tychże punktach. PS. Z definicji liczysz pochodne w x₀ = 0 i x₀ = 2

ktoś: Okej teraz juz rozumiem. Ogólnie czy stwierdzenie ze z 'wygladu' funkcji czyli przez ostrą krawędź w punkcie 2, funkcja nie może być różniczkowalna w (−oo, oo) jest wystarczające?

ktoś: I ostatnie pytanie czy muszę te pochodne liczyć z definicji czy mogę normalnie?

kochanus_niepospolitus: Taka argumentacja może jedynie posłużyć do powiedzenia, dlaczego badasz pochodną z definicji właśnie w tych dwóch punktach. Już prędzej (dodając odpowiednią argumentację) rysujesz dwie proste przechodzące przez punkt (2,10) będące styczne do funkcji f(x). Pokazujesz, że mają (te styczne) różne współczynniki kierunkowe (kąt nachylenia z osią OX) co winno być niczym innym jak pochodną funkcji f(x) w punkcie x₀=2. Wniosek − f(x) nie jest różniczkowalna w tymże punkcie (ponieważ posiada nieskończenie wiele stycznych w tymże punkcie).

kochanus_niepospolitus: Żeby to miało "ręce i nogi" powinno się liczyć z definicji granicę lewo i prawostronną.

ktoś: Okej dzięki