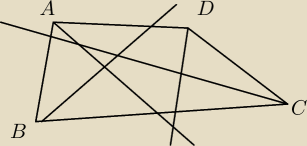
Wykaz że jeśli w dowolnym czworokącie ABCD dwusieczne kątów wewnętrznych wyznaczają
czworokąt(zobacz rysunek obok) to można na nim opisac okrąg
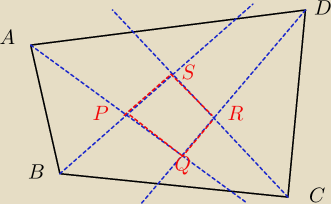przykładowe sformułowanie
założenia:
∡BAP = ∡PAD =α , ∡CBP = ∡ABP = β
∡BCR = ∡DCR = γ , ∡CDR = ∡ADR = δ są to dwusieczne kątów wewnętrznych
P≠Q≠R≠S wyznaczają czworokąt
tezy:
∡PQR + ∡PSR = 180°
∡SPQ + ∡SRQ = 180°
sumy przeciwległych kątów wewnętrznych czworokąta PQRS są równe 180°