wykres arcctg ola: Wykres arcctg Dobry wieczór, mam pytanie. Otóż mam narysować wykresy następującej funkcji: f(x)=arcctg|(x²−2x−3)/x−3| . Czy jest jakiś inny sposób niż podstawianie za x argumentów charakterystycznych arcctg i z tego rysowanie? Jeśli jest to pewnie trzeba przekształcić to wyrażenie w wartości bezwzględnej−tylko jak?Proszę o pomoc

Pytający: (−1,π/2) Zgaduję, że chodzi o funkcję:

	x2−2x−3
f(x)=arcctg|		|,
	x−3

a nie jak wynika z Twojego zapisu (kwestia braku nawiasu):

	x2−2x−3
f(x)=arcctg|		−3|.
	x

Zatem:

	x2−2x−3		(x−3)(x+1)
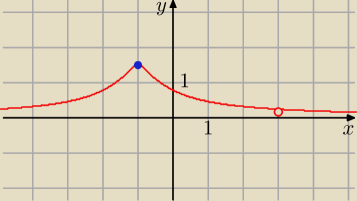
f(x)=arcctg|		|=arcctg|		|=arcctg|x+1| dla x≠3 (dziedzina)
	x−3		x−3

Zatem dla x≥−1 masz zwykły wykres arcusa cotangensa przesunięty o 1 w lewo, natomiast x=−1 jest osią symetrii, czyli dla x<−1 masz odbicie lustrzane tego po prawej, co widać wyżej. Oczywiście x=3 wyrzucasz ze względu na dziedzinę.