Równanie stycznej
Desu: Napisać równanie stycznej do wykresu funkcji f(x)=x2+2 w punkcie P(3,f(3)).
6 gru 19:40
Eta:
f(3)=9+2= 11
f'(x)=2x to f'(3)=6
styczna ma równanie
y= f'(3)(x−3)+f(3)
y= 6(x−3)+11
y=6x+7
6 gru 19:43
Desu: Bardzo dziękuję. Odpowiedź poprawna tylko zły znak na końcu. Powinno być y=6x−7
6 gru 19:47
Eta:
Chochlik
y=6x−7
6 gru 19:48
Janek191:
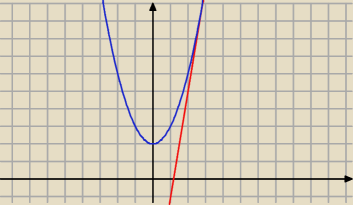
f(x) = x
2 + 2
więc
f '(x) = 2 x
a = f '(3) = 6
f(3) = 3
2 + 2 = 11
y = a x + b
y = 6 x + b oraz P = ( 3, 11)
11 = 6*3 + b ⇒ b = − 7
Odp. y = 6 x − 7
================
6 gru 19:49
Eta:

6 gru 19:50
Eta:
@
Janka
W tablicach maturalnych widnieje wzór:
styczna ma równanie: y= f
'(x
o)(x−x
o)+y
o , P(x
o,y
o) −−− punkt styczności
bez żadnych "b"

6 gru 19:52
Janek191:
Nie zaglądam do tablic maturalnych


6 gru 19:54
Eta:
To zajrzyj

6 gru 19:57
 f(x) = x2 + 2
więc
f '(x) = 2 x
a = f '(3) = 6
f(3) = 32 + 2 = 11
y = a x + b
y = 6 x + b oraz P = ( 3, 11)
11 = 6*3 + b ⇒ b = − 7
Odp. y = 6 x − 7
================
f(x) = x2 + 2
więc
f '(x) = 2 x
a = f '(3) = 6
f(3) = 32 + 2 = 11
y = a x + b
y = 6 x + b oraz P = ( 3, 11)
11 = 6*3 + b ⇒ b = − 7
Odp. y = 6 x − 7
================




