rachunek różniczkowy
nahh: Uzasadnij ,że równanie ma przynajmniej 1 rozwiązanie
x5+x2−4=0, <1;2>
Wiem, że można to rozwiązać za pomocą tw. Darboux'a, ale mam to zadanie w dziale
z rachunku różniczkowego, a o tym twierdzeniu nie było nigdzie wspomniane, więc prosiłabym,
aby tak tego nie rozwiązywać
6 gru 18:31
Eta:
x
5= −x
2+4
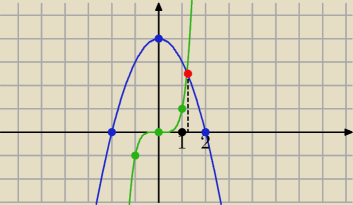
Można narysować dwa wykresy
y= −x
2+4
i
y= x
5
w przedziale x∊<1,2> wykresy mają jeden punkt wspólny
6 gru 22:49
Eta:
2 sposób
Za pomocą pochodnych..........
6 gru 22:50
nahh: w jaki sposób za pomocą pochodnych
6 gru 23:32
kochanus_niepospolitus:
1) wykazujesz, że f(x) = x5 jest funkcją rosnącą
2) wykazujesz, że g(x) = −x2+4 jest funkcją malejącą na przedziale (1,2)
3) pokazujesz f(2) > g(1) > f(1)
Jednak na dobrą sprawę to także jest coś a'la tw. Darboux'a
6 gru 23:38
Eta:

6 gru 23:39
 x5= −x2+4
Można narysować dwa wykresy
y= −x2+4
i y= x5
w przedziale x∊<1,2> wykresy mają jeden punkt wspólny
x5= −x2+4
Można narysować dwa wykresy
y= −x2+4
i y= x5
w przedziale x∊<1,2> wykresy mają jeden punkt wspólny
