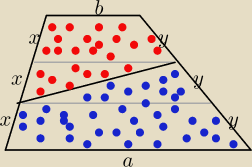
trapez matma: Mam obliczyć stosunek pól czerwonego do niebieskiego

	7b+2a
Odp:
	7a+2b

Mila:

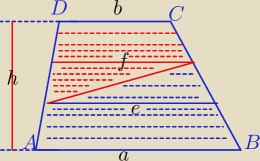
	a+f		e+b
e=		i f=		⇔2e=a+f i 2f=e+b⇔f=2e−a
	2		2

−−−−−−−−−−−−−−−−− 2*(2e−a)=e+b⇔4e−2a=e+b

	2a+b
e=
	3

===========

	a+e		h		1		h
Pn=		*		+		e*
	2		3		2		3

	7a+2b
Pn=		*h
	18

	a+b		a+b		7a+2b
Pc=		*h−Pn=		*h−		*h
	2		2		18

	9a+9b−7a−2b		2a+7b
Pc=h*		=		*h
	18		18

Pc		2a+7b
	=
Pn		7a+2b

========================

betka: Oznaczam poprzeczne odcinki − idąc od dołu c oraz d. Wysokości wszystkich trzech pasków trapezu muszą być równej długości (to wynika z twierdzenia Talesa) − oznaczam je "z". Każde z pól : czerwone i niebieskie to suma pola trapezu i trójkąta, każda z figur ma wysokość z. Uwaga: czerwony trójkąt jest rozwartokątny i jego wysokość poprowadź na przedłużenie odcinka d poza trapez.

(b+d)*z   d*z   + 2   2
(a+c)*z   c*z   + 2   2

betka: Wystarczy ułamek skrócić przez z, rozszerzyć przez 2 i dostaniesz

b+2d
	(*)
a+2c

Następnie z własności odcinków środkowych trapezu mamy:

	d+a		b+c
c=		oraz d=
	2		2

co przekształcając otrzymujemy

	2		1
d =		b +		a
	3		3

	1		1
c=		d+		a
	2		2

Te wyrażenia podstaw do (*) i koniec.

Eta: @betka Mila napisała to, o czym Ty piszesz z tą różnicą,że podała rozwiązanie bardzo przejrzyste wraz z rysunkiem i "koniec"