ss Izzy: lim x −−−> 0

sinx
	= 1
x

	x
czy		= 1
	sinx

?

5-latek: A nie mozna zobaczyc w ksiazce jak jest ?

Izzy: W jakiej?

5-latek: W kazdej ksiazce do analizy matematycznej

Adamm:

	sinx
limx→0		= 1 <− dowód jest geometryczny
	x

z tw. o arytmetyce granic

	1		x
limx→0		= limx→0		= 1
	sinx   x		sinx

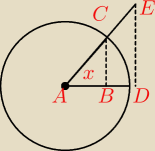
Adamm: dla π/2>x>0 na okręgu jednostkowym zataczamy kąt x długość łuku: x długość boku BC: sinx długość boku ED: tgx zatem mamy nierówności sinx<x<tgx dla π/2>x>0 stąd

	sinx
cosx<		<1 dla π/2>x>0
	x

dla π/2>−x>0 czyli dla −π/2<x<0 mamy

	sin(−x)
cos(−x)<		<1
	−x

czyli inaczej

	sinx
cosx<		<1
	x

teraz na mocy twierdzenia o 3 funkcjach

	sinx
limx→0		= 1
	x

jc: Dobry wieczór 5−latku, Akurat w 2 z 3 książek z analizy, jakie posiadam, nie ma takiego dowodu. W obu wspomnianych autorzy definiują sinus za pomocą szeregu potęgowego. Powyższa granica jest wnioskiem nie wartym uwagi.

Adamm: jc wcześniej użyłeś tego słowa "elementarny" więc uznaj ten dowód za "elementarny"

5-latek: Dobry wieczor jc ) jest on w mojej starej ksiazce do 3 klasy technikum I tez tak mysle jak Ty ze skoro ktos nie jest na studiach nauczycielskich to wystarczy znac tylko taka granice .

Izzy: Dziękuje mistrzowie

jc: Sam zwykle przedstawiam ten rysunkowy dowód.

Mariusz: Zobacz jak to jest w książkach dostępnych za darmo w sieci http://matwbn-old.icm.edu.pl/kstresc.php?tom=15&wyd=10&jez=pl http://kielich.amu.edu.pl/Stefan_Banach/rachunek.html No tutaj najbardziej pomógł Adaś , dobra robota