zadanie z rombem/wektorami/prostymi Mathem: Punkt A = (1; −2) jest wierzcholkiem rombu, ktorego jeden z bokow zawiera sie w prostej k o rownaniu x−y−3 = 0; natomiast punkt O = (2; 2) jest srodkiem symetrii tego rombu. a) Wyznacz wspolrzedne pozostalych wierzcholkow tego rombu. b) Oblicz pole tego rombu. c) Znajdz kosinus kata ostrego tego rombu.

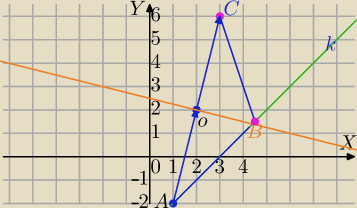
Mila: k: x−y−3 = 0⇔y=x−3 1) AO^→=[1,4] O(2,2)→T_[1,4]⇒C=(3,6) 2) BD⊥AC AC: y=ax+b −2=a+b 2=2a+b⇔a=4 BD:

	1
y=−		x+b i O należy do prostej BD
	4

	1		5
2=−		*2+b, ⇔b=
	4		2

	1		5
y=−		x+
	4		2

3) B− punkt przecięcia prostej k przekątnej BD

	1		5
−		x+		=x−3
	4		2

	22		8
x=		, y=
	5		5

	22		8
B=(		,		)
	5		5

Pozostało Ci obliczyć wsp. punktu D Próbuj dalej sam.