Oblicz pole trójkąta, powstałego z punktów umieszczonych na szescianie... Michał: Hej Potrzebuje wsparcie w lieczniu, gdyby ktoś mógł pomoc będę wdzięczny. Dany jest sześcian ABCDA'B'C'D' o krawędzi 24. Oblicz pole trójkąta BDE, gdzie punkt E należy do krawędzi CC' i dzieli ją w stosunku 3:5, licząc od dolnej podstawy. a=24 stosunek 3x 5x 3x+5x=24 x=3 3x=9 9=|CE|=b 9²+24²=x² (|DE|) wychodzi x=√657=3√63 Teraz |DE|=|BE| czyli trójkąta którego pole musimy policzyć jest trójkątem równoramiennym. z czego jego podstawa |DB| = przekątna kwadratu o boku 24 ( a√2) czyli 24√2 podstawe dzieli wysokość na dwie równe częsci... 12√2. Z pitagorasa obliczam h trójkąta. (12√2)²+h²=657 657−288=h² h²=369 h=3√123 Teraz P trójkata = 24{2}*3√123*¹₂=36√246 Oki to tak liczę to co liczę.... Problem w tym że odp wynosi P=36√46 Moje pytanie gdzie jest błąd ? PS. Znazłem na forum wątek o tym zadanku... Niestety osoby biorące udział w dyskusji okazały się sprytniejsze niż ja i nie rozumiem jak im to wyszło co im wyszlo. Wątku nie mogłem odświeżyć za pewne został zamknięty przez administratora więc stworzyłem nowy Przperaszam za problem jak by co Oprócz tego drugie zadanie też jakiś błąd dziki, chyba obliczeniowy... Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny jego podstawy pod kątem takim że sin α=³₅. Pole koła wpisnaego w podstawę jest równe 36π. Wyznacz objętość ostrosłupa. a−krawedz podstawy h−wysokosc podstawy ok r=a√3/2 z tego liczę a (a√3/6)² *π=36π a=12√3 h=18 ²₃h=12 Oki teraz sin cos sin²α+cos²α=1 cos²α=⁴₅ (po podstawieniu) tgα=sinα/cosα=³₄ I teraz z funkcji trygonometrycznej tgα=^H₁₂ H=9// Tutaj robie bład według roziwazania bo ma być 9/2

	(12√3)2*p(3)
V=13 *		*9=324√3 //Zła odp ma być 162√3 czyli to przez to źle
	4

wyliczone H Ale w którym miejscu?... Przeciez 36/4 =9 Proszę o wsparcie i za pomoc z góry dziękuję. Pozdrawiam

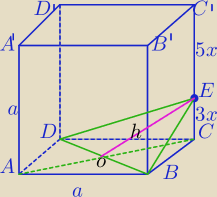Mila: 3x+5x=8x 8x=24 x=3 |CE|=9

	1
PΔBDE=		|BD|*h
	2

|BD|=24√2 W ΔOEC: h²=9²+(12√2)² h²=81+144*2⇔h²=369 h²=9*41 h=3√41 P_Δ=12*3√41=36√41 ==========

Mila: zgubiłam √2 P_Δ=12√2*3√41=36√82

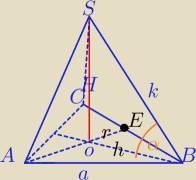Mila: II też masz dobrze, ale można prościej rozwiązać. 1) π*r²=36π⇔r=6 h=18, |OB|=12

a√3
	=18⇔a√3=36⇔3a=36√3
2

a=12√3 2)W ΔSOB:

	3		H		3		5H
sinα=		⇔		=		⇔k=
	5		k		5		3

k²=|OB|²+H²

	5H
(		)2=122+H2
	3

	9
H2=144*
	16

	3
H=12*		⇔H=9
	4

	1		1
V=		*(		*12√3*18)*9
	3		2

V=324√3 ========

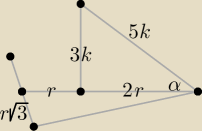Bogdan: Moja propozycja πr² = 36π ⇒ r = 6, 3r = 18, r√3 = 6√3 2r = 12 = √ 25k² − 9k² = 4k ⇒ k = 3, 3k = 9

	1
Objętość V =		*6√3*18*9 = 324√3
	3

Eta:

Michał: Dzięki =) za pomoc Mila i Bogdan. Za rozpisanie i pokazania wersji drugiej zadania drugiego Doceniam i pozdrawiam cieplutko.