jednokładność i pobobieństwo, twierdzenie talesa korky: 5 zadań. jednokładność i pobobieństwo, twierdzenie talesa. bardzo prosze o pomoc w rozwiązaniu tych zadań... 1. W trapezie ABCD, gdzie AB||CD, |AB|=14cm, |CD|=3,5 cm, |AD|=6 cm, przedłużono ramiona AD i BC do przecięcia w punkcie E. Oblicz |DE|. 2. W trapezie równoramiennym długość wysokości wynosi 14 cm, przekątne są do siebie prostopadłe, a ich punkt wspólny dzieli każdą w stosunku 1:3. Oblicz obwód trapezu. 3. W równoległoboku, którego obwód jest równy 48 cm, stosunek wysokości wynosi 3:5. Oblicz długość boków tego równoległoboku. 4. Pole trapezu jest równe 120 cm2, a stosunek długości podstaw wynosi 1:3. W trapezie tym poprowadzono przekątne, które podzieliły trapez na cztery trójkąty. Oblicz pola tych trójkątów. 5. W trapezie ABCD, AB || CD, poprowadzono przekątne AC i BD, które przeciąły się w punkcie S. Pole trójkąta ABS jest równe 18cm2, a pole trójkąta CDS jest równe 8 cm2. Oblicz pole trapezu ABCD.

korky: podbijammmm

jo:

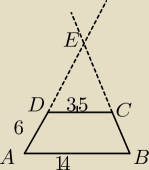
|DE|		|DE|+6
	=		⇒ 14 |DE| = 3,5 |DE| + 21 ⇒ |DE| = 2
3,5		14

korky: dziękować

jo: W poleceniu 3 nie ma części zdania − stosunek wysokości... wynosi...

korky: 3 jest całe przepisałem identycznie jak w zbiorze jest. nawet się teraz upewniałem...

jo: ok

korky: ktoś pomoże może jeszcze?

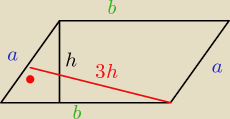
Godzio: 2a+2b = 48 a+b = 24 3h*a = hb a+b = 24 3ha − hb = 0 a+b = 24 h(3a − b) = 0 => h≠0 , 3a−b =0 a+b = 24 3a−b = 0 + −−−−−−−−−−−−−− 4a = 24 a=6 b=18 myśle że tak jest porawnie

Godzio: można jeszcze sprawdzić czy się wszystko zgadza 3h = h₁ h = h₂ zał . h₁ > h₂ ah₁ = bh₂ 6h₁ = 18h₂

h1		3
	=
h2		1

czyli wszystko ok

korky: dzięki

oi:

ziom: Dobrze głodzio zrobił te 3 zadanie? Stosunek wysokosci wyosci 3:5 a u niego jedna wysoskosc to h a druga 3h, to chyba sie nie zgadza