:/ trudne zadanie : Dany jest trójkąt ABC. Niech H będzie jego ortocentrum, O środkiem okregu opisanego, S środkiem ciężkości, F środkiem okręgu przechodzącego przez spodki wysokości trójkąta ABC. Wtedy: A) punkty H, F, O, S leżą na jednej prostej B) odległość punktu F od śródka odcinka CH jest dwa razy mniejsza niż odległość punktu O od punktu B C) długość odcinka HO jest 6 razy większa niz długość odcinka FS D) okrąg przechodzący przez środki odcinków AH, BH, CH jest styczny do okręgu wpisanego w trójkąt ABC

trudne zadanie : Przypomnę się bo wazne dla mnie to zadanie

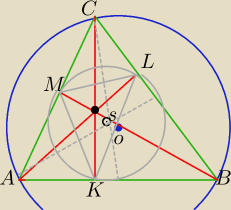
Mila: Trudno narysować dokładny rysunek. Spróbuj na kartce zrobić duży rysunek. 1) W dowolnym trójkącie środek ciężkości (S), środek okręgu opisanego (O), środek okręgu przechodzącego przez środki boków i ortocentrum (H) są współliniowe. 2)Środek okręgu dziewięciu punktów leży na tzw. prostej Eulera, dokładnie w połowie odcinka pomiędzy ortocentrum tego trójkąta a środkiem okręgu na nim opisanego. Tu masz opisane zależności: https://pl.wikipedia.org/wiki/Okr%C4%85g_dziewi%C4%99ciu_punkt%C3%B3w

jc: Przy okazji, trójkąt KLM ma najmniejszy obwód ze wszystkich trójkątów, których wierzchołki leżą na bokach dużego trójkąta. Wysokości dużego trójkąta są dwusiecznymi kątów małego trójkąta.

Mila: tak, to ciekawe własności.