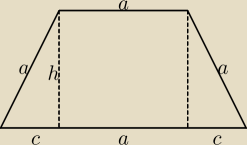
 h = √ a2 − c2
Pole trapezu P = (a + c)*h = (a + c)*√ a2 − c2 = √ (a2 − c2)*(a + c)2
f(c) = (a2 − c2)*(a + c)2
P jest największe dla tej wartości a, dla której funkcja f(c) osiąga maksimum
h = √ a2 − c2
Pole trapezu P = (a + c)*h = (a + c)*√ a2 − c2 = √ (a2 − c2)*(a + c)2
f(c) = (a2 − c2)*(a + c)2
P jest największe dla tej wartości a, dla której funkcja f(c) osiąga maksimum
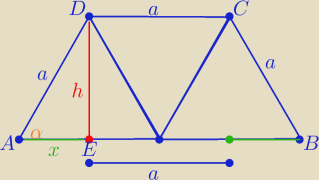 Takim trapezem jest trapez "sklejony z trzech trójkątów równobocznych o boku dł. "a"
wykażemy to:
|AE|= x |AB|=a+2x , |DC|=a
P= (a+x)*h
x= a*cosα i h= a*sinα
P(α)= (a+acosα)*asinα ⇒ P(α)= a2sinα*(1+cosα) ,
P'(α)=a2[cosα(1+cosα)+sinα*(−sinα)
P'(α)=0 ⇔ cosα+cos2α−sin2α=0 , sin2α= 1−cos2α
2cos2α+cosα−1=0 Δ=9 √Δ=3
........................................
........................................
α=60o
=======
................................
Takim trapezem jest trapez "sklejony z trzech trójkątów równobocznych o boku dł. "a"
wykażemy to:
|AE|= x |AB|=a+2x , |DC|=a
P= (a+x)*h
x= a*cosα i h= a*sinα
P(α)= (a+acosα)*asinα ⇒ P(α)= a2sinα*(1+cosα) ,
P'(α)=a2[cosα(1+cosα)+sinα*(−sinα)
P'(α)=0 ⇔ cosα+cos2α−sin2α=0 , sin2α= 1−cos2α
2cos2α+cosα−1=0 Δ=9 √Δ=3
........................................
........................................
α=60o
=======
................................
| a2√3 | ||
P= 3* | −−− pole maksymalne | |
| 4 |


