przybywam z zadaniem
przybysz daleki: W półkole o promieniu R wpisano trapez równoramienny tak, że jego dłuższa podstawa pokrywa się
ze średnicą pólkola oraz wiadomol, że da się w niego wpisać okrąg. Oblicz długość krótszej
podstawy trapezu.
3 gru 18:09
Eta:
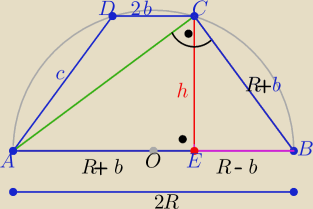
Trapez równoramienny o podstawach 2R i 2b
|AE|=R+b , |EB|=R−b , b∊(0,R)
Z warunku wpisania okręgu w trapez
2R+2b=2c ⇒ c=R+b
W trójkącie prostokątnym ABC : h
2=(R−b)(R+b) ⇒ h
2=R
2−b
2
i z tw. Pitagorasa w Δ EBC
(R+b)
2=h
2+(R−b)
2 .
...........................
b
2+4Rb−R
2=0
Δ
b= 16R
2+4R
2 =20R
2 ,
√Δ=2
√5R
b= R
√5−2R >0 ( druga wartość b <0
===========
3 gru 19:19
Eta:
Popraw wynik:
2b= 2R√5−4R = 2R(√5−2)
3 gru 19:26
Mila:

3 gru 19:34
Eta:
Hej Mila
Coś nie tak?
3 gru 19:49
Mila:
Wszystko pięknie, mam ten sam wynik

Napisałaś wcześniej, to nie wpisałam rozwiązania.
3 gru 21:16
Eta:

3 gru 21:17
 Trapez równoramienny o podstawach 2R i 2b
|AE|=R+b , |EB|=R−b , b∊(0,R)
Z warunku wpisania okręgu w trapez
2R+2b=2c ⇒ c=R+b
W trójkącie prostokątnym ABC : h2=(R−b)(R+b) ⇒ h2=R2−b2
i z tw. Pitagorasa w Δ EBC
(R+b)2=h2+(R−b)2 .
...........................
b2+4Rb−R2=0
Δb= 16R2+4R2 =20R2 ,√Δ=2√5R
b= R√5−2R >0 ( druga wartość b <0
===========
Trapez równoramienny o podstawach 2R i 2b
|AE|=R+b , |EB|=R−b , b∊(0,R)
Z warunku wpisania okręgu w trapez
2R+2b=2c ⇒ c=R+b
W trójkącie prostokątnym ABC : h2=(R−b)(R+b) ⇒ h2=R2−b2
i z tw. Pitagorasa w Δ EBC
(R+b)2=h2+(R−b)2 .
...........................
b2+4Rb−R2=0
Δb= 16R2+4R2 =20R2 ,√Δ=2√5R
b= R√5−2R >0 ( druga wartość b <0
===========

 Napisałaś wcześniej, to nie wpisałam rozwiązania.
Napisałaś wcześniej, to nie wpisałam rozwiązania.
