Przedstawiam takie oto zadanko inga: Trapez równoramienny, opisany na okręgu, ma dłuższą podstawę długości a i kąt ostry przy podstawie α. Oblicz długość przekątnej tego trapezu.

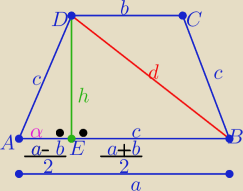
Eta: 1/ z warunku wpisania okręgu w trapez:

	a+b
a+b=2c ⇒		=c
	2

2/ wΔABE: h=c*sinα i a−b=2c*cosα a+b= 2c + −−−−−−−−−−−−−−−

	a		a*sinα
a=c(cosα+1) ⇒ c=		i h=
	cosα+1		cosα+1

3/ z tw. Pitagorasa w ΔBED: d²=h²+c²

	a2sin2α +a2
d2=
	(cosα+1)2

	a
d=		*√sin2α+1 [j]
	cosα+1

=====================