Geometria analityczna
Ola: Mam takie dwa okręgi
(x−3)2 + (y−3)2 = 5
(x−4)2 + (y−1)2 = 16
Należy znaleźć taki punkt na osi OX aby długości stycznych poprowadzonych z tego punktu do tych
okręgów bbyły równe
Odp to (−6,0)
3 gru 14:38
iteRacj@:
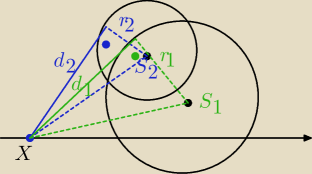
okręgi
(x−3)
2 + (y−3)
2 = 5 S
2(3,3) r =
√5
(x−4)2 + (y−1)2 = 16 S
1(4,1) r = 4
X (x
o, 0) szukany pkt na osi OX
d
1 długość odcinka poprowadzonego z punktu X do pktu styczności z okregiem o śrd S
1
d
2 długość odcinka poprowadzonego z punktu X do pktu styczności z okręgiem o śrd S
2
d
1 = d
2
z tw. Pitagorasa |XS
1|
2 = (r
1)
2 + (d
1)
2 oraz |XS
2|
2 = (r
2)
2 + (d
2)
2
(d
1)
2 = |XS
1|
2 − (r
1)
2
(d
2)
2 = |XS
2|
2 − (r
2)
2
podstawiam dane
(d
1)
2 = (4−x
o)
2+(1−0)
2 − (r
1)
2
(d
2)
2 = (3−x
o)
2+(3−0)
2 − (r
2)
2
(d
1)
2 = (4−x
o)
2+1 − 16
(d
2)
2 = (3−x
o)
2+9 − 5
(4−x
o)
2+1 − 16 = (3−x
o)
2+9 − 5
po obliczeniu x
o = −6
3 gru 15:52
Ola: Dziekuje ❤️
3 gru 16:46
 okręgi
(x−3)2 + (y−3)2 = 5 S2(3,3) r = √5
(x−4)2 + (y−1)2 = 16 S1(4,1) r = 4
X (xo, 0) szukany pkt na osi OX
d1 długość odcinka poprowadzonego z punktu X do pktu styczności z okregiem o śrd S1
d2 długość odcinka poprowadzonego z punktu X do pktu styczności z okręgiem o śrd S2
d1 = d2
z tw. Pitagorasa |XS1|2 = (r1)2 + (d1)2 oraz |XS2|2 = (r2)2 + (d2)2
(d1)2 = |XS1|2 − (r1)2
(d2)2 = |XS2|2 − (r2)2
podstawiam dane
(d1)2 = (4−xo)2+(1−0)2 − (r1)2
(d2)2 = (3−xo)2+(3−0)2 − (r2)2
(d1)2 = (4−xo)2+1 − 16
(d2)2 = (3−xo)2+9 − 5
(4−xo)2+1 − 16 = (3−xo)2+9 − 5
po obliczeniu xo = −6
okręgi
(x−3)2 + (y−3)2 = 5 S2(3,3) r = √5
(x−4)2 + (y−1)2 = 16 S1(4,1) r = 4
X (xo, 0) szukany pkt na osi OX
d1 długość odcinka poprowadzonego z punktu X do pktu styczności z okregiem o śrd S1
d2 długość odcinka poprowadzonego z punktu X do pktu styczności z okręgiem o śrd S2
d1 = d2
z tw. Pitagorasa |XS1|2 = (r1)2 + (d1)2 oraz |XS2|2 = (r2)2 + (d2)2
(d1)2 = |XS1|2 − (r1)2
(d2)2 = |XS2|2 − (r2)2
podstawiam dane
(d1)2 = (4−xo)2+(1−0)2 − (r1)2
(d2)2 = (3−xo)2+(3−0)2 − (r2)2
(d1)2 = (4−xo)2+1 − 16
(d2)2 = (3−xo)2+9 − 5
(4−xo)2+1 − 16 = (3−xo)2+9 − 5
po obliczeniu xo = −6