Wykaż, że funkcja f(x) x+2/x-1 KamiL: Wykaż, że funkcja f(x) = x+2/x−1 a)jest malejąca w przedziale (−∞,1) b)nie jest malejąca w zbiorze R /{1}

jc: Spytaj Wolframa.

KamiL: W odejmowaniu f(x1) −f(x2) wychodzi mi postać −3(x1−x2)/(x1−1)(x2−1) i nie wiem co z tym robić, zarówno w przykładzie a jak i b. Jak skończyć te dowody?

jc: Tak mała sugestia, masz 26 liter, potrzebujesz dwóch, a dopisujesz indeksy. f(a)−f(b)=a+2/a−b−2/b = (a−b)(1−2/ab)

5-latek: x₁<x₂ to f(x₁)>f(x₂) x₁−x₂<0 to f(x₁)−f(x₂)>0 ja by doprowadzil funkcje do takiej postaci

	(x−1)+3		3
y=		= 1+
	x−1		x−1

5-latek: Dobry wieczor jc Mecze twierdzenie Stolza .

KamiL: dziękuję za odp, tylko nie bardzo rozumiem, np w podpunkcie a mam założenie, że x1>x2, x1−x2>0 i wtedy f(x1)>f(x2)? Skąd Twoje założenia ?

KamiL: czy mógłbym prosić o bardziej stopniowe wytłumaczenie, bo chciałbym wiedzieć, gdzie robię błąd, bo może już na etapie założeń

5-latek: Funkcja jest maljaca jesli dla mniejszsego argumentu przyjmuje wieksza wartosc

5-latek:

	3		3
1+		−(1+		)>0
	x1−1		x2−1

3		3
	−		>0
x1−1		x2−1

3(x2−1)−3(x1−1
	>0
x1−1)(x2−1)

3[(x2−1)−(x1−1)]
	>0
(x1−1)(x2−1)

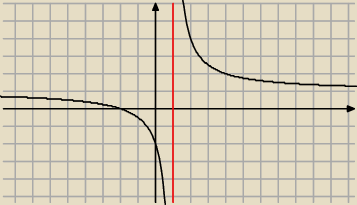
Teraz analiza x₁−1 <0 x₂−1<0 Iloczyn dwoch licz ujemnych jest dodatni (czyli mianownik jest dodatni teraz licznik skoro x₁−x₂<0 to x₂−x₁>0 czyli licznik dodatni czyli caly ten ulamek jest dodatni wiec funkcja na przedziale (−∞ 1) jest malejaca co potwierdza wykres tej funkcji

jc: Dla ujemnych x, możemy napisać x+2/x−1 = −(√−x − √−2/x)² − 2√2−1, skąd wynika, że funkcja rośnie dla x ≤ −√2, a potem maleje.

jc: 5−latku, piszesz o zupełnie innej funkcji.

5-latek: tak nie ma nawiasow . Chyba zcas zrobic mocniejszse okulary .

KamiL: Dziękuję, ten 1 przykład rozpisany przez 5−latka już w miarę rozumiem. Ale co w przypadku gdy nie możemy określić znaku (x1−1)(x2−1), bo rozpatryjemy zbiór liczb rzeczywistych bez 1?

KamiL: Czy przykład b powinno się rozwiązać licząc p i q a potem pogladowo tworząc rysunek?