Równoległobok
Peet: Kąt ostry równoległoboku ma miarę 30 st. Przekątne równoległoboku przecinają się w punkcie S
oddalonym od jego boków odpowiednio o 4 cm i 12 cm. Oblicz długość krótszej przekątnej
równoległoboku.
2 gru 15:02
Eta:
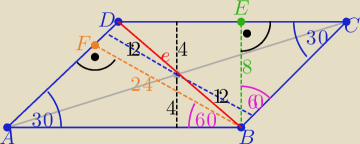
Rysunek......
1/ w Δ ABE .....|AB|=48
w Δ BCE ... |BC|=16
2/ Z tw. cosinusów w ΔABC
e
2= 48
2+16
2−2*48*16*cos30
o
..........................
e=...................
2 gru 15:29
Peet: Kosmiczny ten rysunek

W BCE wiem że tam jest trójkat 30 60 i 90 i zależnosci między nimi dlatego BC=16
Ale jak policzyć ABE, że AB wyszło 48 ?
2 gru 15:41
Eta:
Jaki "kosmiczny"

Δ ABE też "ekierka" o katach 30
o,60
o,90
o
|BE|=24 to |AB|=2*24=...
2 gru 15:49
Peet: W ogóle twierdzenie cosinusów w ABC nie pozwoli nam policzyć e tylko |AC| czy się mylę ?
2 gru 15:51
Eta:
Δ ABF miało być
2 gru 15:51
Eta:
Co Ty wymyślasz?
Poczytaj o tw. kosinusów
2 gru 15:52
Janek191:
Na rysunku pisze,że I BE I = 8 ?
2 gru 15:53
Peet: Jeżeli kąt przy A ma 30 stopni i poprowadzi się prostą z niego do E to ten kąt chyba musi być
mniejszy niż 30 ? Więc ekierka nie wyjdzie ?
2 gru 15:54
Eta:
Po przesunięciu też masz trójkąt prostokątny z jednym kątem 30
o
to jaką miarę ma drugi kąt w takim trójkącie ? jasne,że 60
o

2 gru 15:55
Eta:
@Janek
O co Ci chodzi? bo nie wiem ?
2 gru 15:56
Eta:
|BE|=4+4=8
2 gru 15:57
Peet: Janek bo tutaj z tego co widzę to jest skopana kolejność i oznaczenia dlatego wychodzą takie
kwiatki
2 gru 15:59
Janek191:
Chodziło mi o wpis z 15.49

2 gru 16:00
Eta:
Poprawiam te chochliki

1/ w ΔAB
E .... |AB|=48
2/ z tw. cosinusów w Δ AB
D
e
2=..........
2 gru 16:02
Eta:
Dzięki już poprawiłam

Oczopląsu można dostać pisząc na kompie i zerkając na rysunek
@
Peet ........ czy już teraz jasne ?
2 gru 16:03
Eta:
I czekam na ładny "kwiatek"

2 gru 16:04
Janek191:

2 gru 16:08
Peet:

@Eta
Teraz wszystko jasne

Dzięki
2 gru 16:10
Eta:


2 gru 16:15
Peet: Jeszcze jedno mam pytanie.
Jeżeli |AD|= 16
To jak to jest możliwe że |AF|=24sqrt3 ?
Gdzie z rysunku wynika że AF jest krótsze
2 gru 16:16
Eta:
2 sposób
P=a*ha=b*hb ⇒ a*8=b*24 ⇒ a=3b ( i zgadza się bo 48=3*16)
i licz dalej.............
2 gru 16:17
Eta:
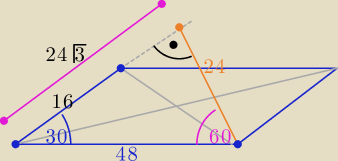
2 gru 16:24
Eta:
Co nie ma wpływu na wyznaczenie długości "e"
e2 = a2+b2−2ab*cos30
e=.........
2 gru 16:27
Peet: Ten rysunek jest OK jak się patrzy na długości
Mnie po prostu zastanawia jak w 1 rysunku możliwe jest to że |AD| = 16 a |AF| około 32 (czyli
jest 2x dłuższy) a zgodnie z rysunkiem powinien być krótszy

2 gru 16:30
Eta:
Mamy wyznaczyć długości boków
W tym równoległoboku :
jedna wysokość ha=8 zawiera się w tym równoległoboku
druga hb jest na zewnątrz równoległoboku
Narysowałam Ci drugi rys. na którym to widać
Nie ma to wpływu na wyznaczenie a i b
2 gru 16:39
Eta:
Jasne?
2 gru 16:52
 Rysunek......
1/ w Δ ABE .....|AB|=48
w Δ BCE ... |BC|=16
2/ Z tw. cosinusów w ΔABC
e2= 482+162−2*48*16*cos30o
..........................
e=...................
Rysunek......
1/ w Δ ABE .....|AB|=48
w Δ BCE ... |BC|=16
2/ Z tw. cosinusów w ΔABC
e2= 482+162−2*48*16*cos30o
..........................
e=...................
 W BCE wiem że tam jest trójkat 30 60 i 90 i zależnosci między nimi dlatego BC=16
Ale jak policzyć ABE, że AB wyszło 48 ?
W BCE wiem że tam jest trójkat 30 60 i 90 i zależnosci między nimi dlatego BC=16
Ale jak policzyć ABE, że AB wyszło 48 ?
 Δ ABE też "ekierka" o katach 30o,60o,90o
|BE|=24 to |AB|=2*24=...
Δ ABE też "ekierka" o katach 30o,60o,90o
|BE|=24 to |AB|=2*24=...


 1/ w ΔABE .... |AB|=48
2/ z tw. cosinusów w Δ ABD
e2=..........
1/ w ΔABE .... |AB|=48
2/ z tw. cosinusów w Δ ABD
e2=..........
 Oczopląsu można dostać pisząc na kompie i zerkając na rysunek
@Peet ........ czy już teraz jasne ?
Oczopląsu można dostać pisząc na kompie i zerkając na rysunek
@Peet ........ czy już teraz jasne ?


 @Eta
Teraz wszystko jasne
@Eta
Teraz wszystko jasne  Dzięki
Dzięki



