Okrąg opisany na czworokącie
Anna: Dane są dwa trójkąty ABC i ACD, że ( < ABC) = 90O i ( < ADC) = 90O. Uzasadnij, że na
czworokącie ABCD można opisać okrąg. Rozpatrz dwa różne przypadki.
O co może chodzić z dwoma przypadkami ?
Rozumiem, że tutaj twierdzenie talesa zachodzi do tego 90+90=180 więc można opisać okrąg a
drugi przypadek ? Jakieś propozycje ?
2 gru 14:43
iteRacj@:
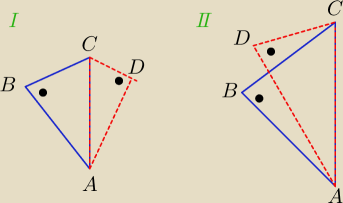
tw. Talesa tu nie stosuj : )
na rysunku kropkami są oznaczone kąty 90
o
moim zdaniem te dwa przypadki tak wyglądają, czy mam rację?
2 gru 16:31
Peet: Przypadek 1 miałem identyczny (i właśnie Talesem wyjaśniłem że można okrąg opisać)
Jak uzasadnić przypadek II że można opisać okrąg ?
2 gru 16:34
iteRacj@:
a jak zastosowałeś tw. Talesa?
2 gru 16:36
iteRacj@:
przypadek II
skorzystaj z tego, że środek okręgu opisanego na trójkącie prostokątnym jest środkiem
przeciwprostokątnej
2 gru 16:38
iteRacj@: w przypadku drugim okrąg opisuję na czworokącie ABDC
2 gru 16:40
Peet: W pierwszy przypadku miałem to na myśli: Twierdzenie Talesa dla okręgu – szczególny przypadek
twierdzenia o kątach wpisanym i środkowym mówiące, że jeśli A, B i C są punktami na okręgu
gdzie odcinek AC jest średnicą, to kąt ABC jest prosty
2 gru 18:11
iteRacj@:
rozumiem,
mam wątpliwość, czy przypadek II, taki jak narysowałam spełnia warunki zadania, bo w treści
jest czworokąt ABCD
2 gru 18:29
Peet: Właśnie dlatego 2 przypadek mnie zastanawia, jak to ma wyglądać ...
2 gru 18:32
Peet: Ale nie da się chyba przedstawić czworokąta ABCD inaczej niż e przypadku nr 1?
2 gru 18:51
Mila:
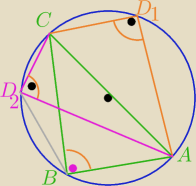
I) sumy kątów przeciwległych mają po 180
o⇔na czworokącie można opisać okrąg
2 gru 18:52
Peet: To są te dwa przypadki ? Z tym różowym wtedy jaka zależność jest spełniona że można na nim
okrąg opisać ? Bo B i D2 raczej nie są przeciwległe ?
2 gru 19:03
 tw. Talesa tu nie stosuj : )
na rysunku kropkami są oznaczone kąty 90o
moim zdaniem te dwa przypadki tak wyglądają, czy mam rację?
tw. Talesa tu nie stosuj : )
na rysunku kropkami są oznaczone kąty 90o
moim zdaniem te dwa przypadki tak wyglądają, czy mam rację?
 I) sumy kątów przeciwległych mają po 180o⇔na czworokącie można opisać okrąg
I) sumy kątów przeciwległych mają po 180o⇔na czworokącie można opisać okrąg