czworokąt mat18: W czworokącie ABCD dane są : |AB|=|AD| oraz kąty przy wierzchołkach A i C są proste Z wierzchołka A poprowadzono wysokość o długości 4 Oblicz pole tego czworokąta I nie mam pomysłu na to zadanie

yht: opisz okrąg o środku S na tym czworokącie bo suma przeciwległych kątów to 180^o |AB|=|AD| = x wówczas trójkąt ABD jest prostokątny i równoramienny, a odcinek |BD| = x*√2 jest też średnicą okręgu opisanego

	x*√2
zatem promień okręgu =
	2

	x*√2
|AS| = |BS| = |CS| = |DS| = r =
	2

trójkąty ABS i ASD też będą prostokątne równoramienne a z tego wynika że BSC i CSD też są trójkątami prostokątnymi i równoramiennymi wówczas |BC| = x i |BD| = x okazało się że czworokąt ABCD jest kwadratem wysokość 4 to jednocześnie bok tego kwadratu P = 16

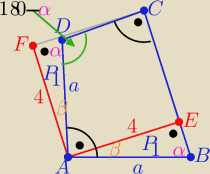Eta: 1/ Na takim czworokącie można opisać okrąg to : |∡ABE|=|∡ADF| zatem trójkąty ABE i ADF są przystające z cechy (bkb) P(ABCD)=P(kwadratuAECF)= 4²=16 [j²] =======