Odpowiedź to 135 stopni Szymon303: Witam mam problem z zadaniem. Liczę już od godziny ale cały czas wychodzi mi zły wynik. Treść zadania brzmi tak: Wyznacz kąt rozwarcia stożka którego tworząca ma długość 10 cm, a pole podstawy jest (50 + 25*√2)π cm²

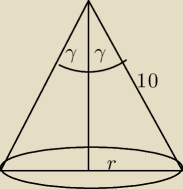
5-latek: πr²= 50+25√2π r²= 50+25 √2 r²= 25(2+√2) r= √25(2+√2 r= 5*√2+√2

	5√2+√2		√2+√2
sinγ=		=		≈0,9239
	10		2

sinγ= 67^o30' 2γ= 135^o

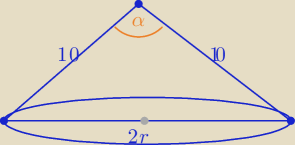
Eta: Z twierdzenia cosinusów

	102+102−(2r)2
cosα=		⇒ 200cosα= 200 −4r2
	2*10*10

z treści zadania : r²=50+25√2

	√2
to 200cosα= −100√2 ⇒ cosα= −		⇒ α=180o−45o
	2

α= 135^o ========

Eta: Hej "małolatku" Nie można stosować przybliżeń

5-latek: Dzien dobry Eta Dlaczego nie ? Z tego co jescze pamietam to zesmy doprowadzali np objetosc do postaci logartmowanej i logarytmy sinusow czy tangensow odczytywali z tablic . Moze teraz nie mozna .

Szymon303: Dziękuję bardzo za rozwiązania

Eta: Doprowadzanie do postaci logarytmicznej to zupełnie co innego ... Tu wartość kąta ma być dokładna Skąd wiesz ,czy γ≈67^o32^'

Eta: @Szymon Jeżeli w trójkącie jest pytanie o miarę kąta W tym przypadku mamy dwa boki i kąt między nimi ⇒ korzystamy z tw, kosinusów

5-latek: Eta Odczytalem z tablic (mam 5 cyfrowe Ale ja to juz rozumiem . Natomiast nie rozumiem za bardzo ciagow i bede o to niebawem pytal