hejo:
musisz przedziałami.
mamy |x+2| , przyrownujemy x+2 do zera, zatem x=−2
teraz |x−3| −−> x−3=0 −> x=3
wiecej wartosci bezwzglednych nie mamy, stad robimy przedzialy
pierwszy od minus nieskonczonosci do tego najmniejszego iksa,
potem od tego iksa do nastepnego najmniejszego itd.
ostatni przedzial jest od ostatniego iksa do nieskonczonosci
i oczywiscie musisz domykac w jakims z przedzialow liczby (procz nieskonczonosci, tam nie
domykasz)
1
o x ∊ (−
∞;−2>
2
o x ∊ (−2;3>
3
o x ∊ (3;
∞)
(zarowno w pierwszym jak i w drugim moglibysmy domknac liczbe −2, wybieramy jeden z nich
ja wybralem ze zawsze sobie z prawej strony domkne)
−− procz nieskonczonosci bo nie znamy konkretnej wartosci nieskonczonosci oczywiscie.
zatem
dla pierwszego przedzialu
1
o x ∊ (−
∞;−2>
|x+2| = −x−2 (podstawiamy za iksa dowolna liczbe z tego przedzialu np. −10, i mamy
|x+2| czyli |−10+2| = |−8| = 8 (musielismy zmienic znak z −8 na 8) czyli jak poczatkowo bylo
x+2 to zmieniamy znak czyli −(x+2) = −x−2
stad dla tego przedzialu |x+2| = − x − 2
teraz jak bedzie z |x−3| ? otoz analogicznie, podstawiajac np. −10 mamy
|−10−3| = |−13| = 13 (znowu znak zmienilismy) czyli
|x−3| = −(x−3) = −x+3
zatem dla tego przedzialu nierownosc wyglada nastepujaco:
4(−x−2) + 4(−x+3) ≤ x + 31
− 4x − 8 − 4x + 12 ≤ x + 31
− 9x ≤ 27
x ≥ − 3
i teraz uwzgledniamy, ze to jest tylko dla przedzialu 1
o czyli x ∊ (−
∞;−2>
zatem x ∊ <−3;−2>
===============
no i teraz juz bedzie bez rozpisywania, czyli tak jak normalnie to sie robi :
2
o x ∊ (−2;3>
4(x+2) + 4(−x+3) ≤ x + 31
4x + 8 − 4x + 12 ≤ x + 31
20 ≤ x +31
x ≥ −11
i uwzgledniajac przedzial:
x ∊ (−2;3>
=========
3
o x ∊ (3;
∞)
4(x+2) + 4(x−3) ≤ x + 31
4x+8+4x−12 ≤ x+31
7x ≤ 35
x ≤ 5
uwzgledniajac 3
o:
x ∊ (3;5>
=======
Rozwiazanie to suma wszystkich wynikowych przedzialow (podkreslilem na czerwono), zatem
x ∊ <−3;5>
 4|x+2| + 4|x−3| ≤ x + 31
4|x+2| + 4|x−3| ≤ x + 31
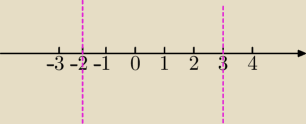 |x+2|=x+2 dla x≥−2
|x+2|=−x−2 dla x<−2
|x−3|=x−3 dla x≥3
|x−3|=−x+3 dla x<3
rozwiązujesz nierówność w 3 przedziałach
|x+2|=x+2 dla x≥−2
|x+2|=−x−2 dla x<−2
|x−3|=x−3 dla x≥3
|x−3|=−x+3 dla x<3
rozwiązujesz nierówność w 3 przedziałach
 Juz wekennd mam
Juz wekennd mam
 Zdrowy?
Zdrowy?
 jestem zdrowy na razie .
jestem zdrowy na razie .