Wyznacz równania ogólne prostych pakoob: Potrzebuję pomocy z końcówką zadania z geometrii analitycznej. W trójkącie ABC dwie wysokości zawierają się w prostych k: x+y−4=0 i l: 2x−y=0. Wyznacz równania ogólne prostych,w których zawierają się boki tego trójkąta, wiedząc, że A(0;2). Wyznaczyłem już z punktu i prostopadłości równania ogólne prostych AB oraz AC, ale nie wiem jak zabrać się za ostatnią prostą − BC. AC: −x+y−2=0 AB: x+y−4=0 Czy ktoś mógłby dać małą wskazówkę?

jc: "wiedząc, że A(0;2)." Wiedząc, że co?

pakoob: Punkt A=(0,2)

jc: Czyli nie są to wysokości zawierające A. Znajdź przecięcia prostych AC i BC z odpowiednimi wysokościami. Będą to punkty B i C.

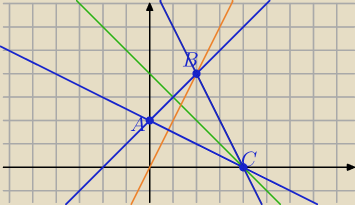
Eta: AB: x−y+2=0 AC: x+2y−4=0 BC: 2x+y−8=0

jc: Wysokość opuszczona z punktu B (tak go oznaczymy): x+y−4=0 Bok AC jest prostopadły do tej wysokości. Zawiera się więc w prostej x−y=−2. Wysokość opuszczona z punktu C 2x−y=0 Bok BC jest do niej prostopadły. Zawiera się więc w prostej x+2y=4. Punkt B. x+2y=4 x+y=4 B=(4,0) Punkt C. x−y=−2 2x−y=0 C=(2,4)

jc: Eta, dlatego w takich zadaniach daję takie dane, że wyniku nie można odczytać z rysunku.

Eta: Hej jc Wiem, wiem Nie odgadywałam ....tylko wyznaczyłam rachunkowo Na rys. tylko sprawdziłam poprawność obliczeń

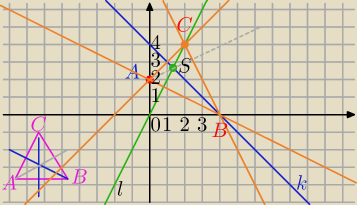
Mila: k: x+y−4=0 i l: 2x−y=0.⇔ k: y=−x+4 l: y=2x 1) Punkt przecięcia: 2x=−x+4 3x=4

	4
x=
	3

	8
y=
	3

	4		8
S=(		,		) − ortocentrum
	3		3

2) AS⊥BC

	8		4		1
AS: y=ax+2 i		=a*		+2⇔a=
	3		3		2

	1
AS: y=		x+2
	2

BC: y=−2x+b , b− wyznaczymy później 3) AB⊥l

	1
AB: y=−		x+b i b=2
	2

	1
y=−		x+2
	2

	1
4) punkt B: −x+4=−		x+2⇔x=4 i y=0
	2

B=(4,0) BC: y=−2x+b i 0=−2*4+b , b=8 BC: y=−2x+8 5) C: −2x+8=2x C=(2,4) AC⊥k y=x+b i 4=2+b, b=2 AC: y=x+2 ===============

jc: Ale skoro widać z rysunku, to po co liczyć?

Eta: Hej Mila Ja liczyłam jak jc z prostopadłości prostych .........