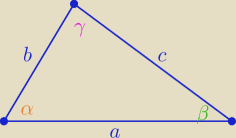
Trójkąt kartydogry: Wykaż, że pole trójkąta jest nie większe od połowy iloczynu dwóch dowolnych jego boków. Nie wiem, jak to zrobić, kombinowalem z wzorem Herona ale nic nie dalo

Mila: Jakie znasz wzory na pole Δ ?

kartydogry: Wszystkie jakie mam w tablicach maturalnych

kartydogry: A może cos z wzorem 1/2 razy a razy b razy sinus?

===: to popatrz na ten z sinusem kąta między bokami

kartydogry: No widzę że jest podobnt i jest blisko, ale jak to opisać?

Eta:

	1
P=		absinα α∊(0o,180o) dla α=90o trójkąt jest prostokątny
	2

	1
sin90o=1 to P=		ab
	2

dla α∊(0^o, 180^o) \ {90^o} trójkąt jest ostrokątny lub rozwartokątny sinα∊(0,1) −− czyli wartości sinusa są ułamkami

	1		1
zatem P=		ab*sinα<		ab
	2		2

łącząc obydwa przypadki otrzymujemy tezę

	1
P≤		ab
	2

podobnie dla boków a, c i kąta β oraz b,c i kąta γ c.n.w

kartydogry: Dziękuję

Eta: I po ptokach sorry ( tym razem ......

Eta: https://matematykaszkolna.pl/forum/363158.html