Rozbicie funkcji oraz narysowanie jej AM: Cześć, mam taką funkcję: f(x)=|−log (|x|−1)+2| f₀(x)=log x f₁(x)=log |x| f₂(x)=log (|x|−1)+2 f₃(x)=−log(|x|−1)+2 f₄(x)=|−log(|x|−1)+2| Czy dobrze to rozbiłem? Ponadto muszę taką funkcję narysować.

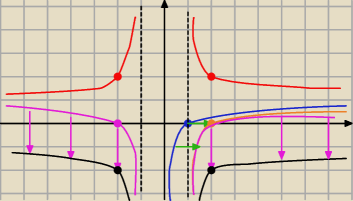
Eta: y=|−log(|x|−1)+2| ⇔ y= |log(|x|−1)−2| , założenie |x|−1>0 ⇒ x∊(−∞, −1) U ( 1, ∞) 1/ y= logx 2 / T_u=[1,0] y=log(x−1) , x>1 3/ Odbicie S_Oy wykresu 2/ y= log(|x|−1) 4/ T_u=[0,−2] y= log(|x|−1)−2 5/ odbicie wykresu 4/spod osi Ox nad oś Ox y= |log(|x|−1)−2|

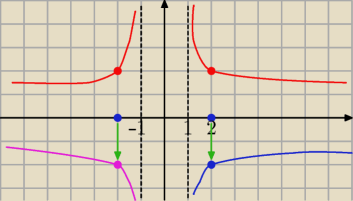Eta: 2 sposób ( łatwiejszy założenie x∊( −∞, −1) U ( 1, ∞) dla x>1 y= |log(x−1)−2| logx T_u=[0,−2 i odbicie spod osi Ox 2/ dla x<−1 y=|log(−x−1)−2| =| log[−(x+1)−2| Obydwie gałęzie to wykres y= |−log(|x|−1)+2|