Rozwiąż nierówność Natalii867: Proszę o pomoc z wytłumaczeniem w rozwiązywaniu tej nierówności.

5−x
	≥ 0
x+1

'Leszek: Po pomnozeniu stronami przez ( x+1)² i x≠−1 (5−x)(x+1) ≥ 0⇒ x ε (−1 , 5)

Żela: Przede wszystkim najpierw dziedzina: x–1≠0 x≠1 D:x∊R\{1} Teraz można przystąpić do zadania. Ponieważ nie wiadomo, czy mianownik jest dodatni, czy ujemny (co zmieniłoby znak nierówności), nie można po prostu pomnożyć stronami. Za to wiadomo, że jeżeli iloraz jest większy/równy 0, to iloczyn również będzie. Stąd: (5–x)(x+1) ≥ 0 5x–x²+5–x ≥ 0 –x²+4x+5 ≥ 0 x²–4x–5 ≤ 0 Δ=4²+4•5=36=6² x=–1 lub x=5 Nierówność ma być mniejsza/równa 0, więc: x∊<–1;5> Lecz przy ostatecznym wyniku należy uwzględnić dziedzinę: x∊<–1;1)∪(1;5>

Żela: Edit: D:x∊R\{–1} Stąd ostateczny wynik powinien być: x∊(–1;5>

Stach: masło maślane (5 − x)(x + 1) = x² − 4x + 5 = (5 − x)(x + 1), x = 5 lub x = −1 (widać przecież od razu)

Natalii867: Dziękuję bardzo !

Stach:

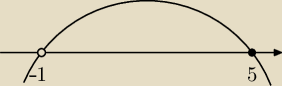
5 − x
	≥ 0 ⇔ −(x − 5)(x + 1) ≥ 0 dla x∊R\{−1}
x + 1

x ∊ (−1, 5>